Оценка качества кластеризации
После создания кластерного решения обычно возникает вопрос, насколько оно устойчиво и статистически значимо. Здесь существует эмпирическое правило – устойчивая группировка должна сохраняться при изменении методов кластеризации: например, если результаты иерархического кластерного анализа имеют долю совпадений более 70% с группировкой по методу средних, то предположение об устойчивости принимается.
В теоретическом плане проблема проверки адекватности кластеризации не решена, по крайней мере, без использования другого вида анализа или априорного знания принадлежности объектов к соответствующим классам. Авторы сборника Ким и др. (1989, с. 192 и далее) подробно рассматривают и в итоге отвергают пять методов проверки адекватности кластеризации (ru.wikipedia.org):
- Кофенетическая корреляция – не рекомендуется и ограниченна в использовании;
- Тесты на значимость разбиения данных на кластеры (многомерный дисперсионный анализ) – всегда дают значимый результат;
- Методика повторных (случайных) выборок – не доказывает обоснованность решения;
- Тесты значимости для признаков, не использованных при кластеризации, – пригодны только при наличии повторных измерений;
- Методы Монте-Карло очень сложны и доступны только опытным математикам.
С тех пор в литературе предложено множество методов и критериев оценки качества результатов кластеризации (clustering validation). Можно выделить несколько подходов к валидации11 кластеров (Kassambara, 2017):
- внешняя валидация, которая заключается в сравнении итогов кластерного анализа с заранее известным результатом (т.е. метки кластеров известны априори);
- относительная валидация, которая оценивает структуру кластеров, изменяя различные параметры одного и того же алгоритма (например, число групп );
- внутренняя валидация, которая использует внутреннюю информацию процесса объединения в кластеры (если внешняя информация отсутствует);
- оценка стабильности объединения в кластеры (или специальная версия внутренней валидации), использующая методы ресэмплинга.
Одна из проблем машинного обучения без учителя состоит в том, что методы кластеризации будут формировать группы, даже если анализируемый набор данных представляет собой полностью случайную структуру. Поэтому первой задачей валидации, которую рекомендуется выполнить перед началом кластерного анализа, является оценка общей предрасположенности имеющихся данных к объединению в кластеры (clustering tendency).
Статистика Хопкинса (Hopkins) является одним из индикаторов тенденции к группированию. Для ее расчета создается B псевдо-наборов данных, сгенерированных случайным образом на основе распределения с тем же стандартным отклонением, что и оригинальный набор данных. Для каждого наблюдения из рассчитывается среднее расстояние до ближайших соседей: между реальными объектами и между искусственными объектами и их самыми близкими реальными соседями. Тогда статистика Хопкинса
Весьма полезна также визуальная оценка тенденции (VAT, Visual Assessment of cluster Tendency): потенциальные группы представлены темными квадратами вдоль главной диагонали “VAT-диаграммы”. Функция get_clust_tendency() из пакета factoextra попутно с графиком рассчитывает также и статистику Хопкинса:
(cluster)
()
df.stand <- ((USArrests))
()
(df.stand, ,
( , ))

Рисунок 10.10: Корреляция между кластеризациями на основе разных методов
(NbClust)
nb <- (df.stand, , ,
, , )
## KL CH Hartigan CCC Scott Marriot TrCovW
## Number_clusters 8.0000 2.000 5.0000 2.000 5.0000 5.0 4.0000
## Value_Index 24.0818 43.462 12.3077 -0.141 43.9763 180497.5 383.4582
## TraceW Friedman Rubin Cindex DB Silhouette Duda
## Number_clusters 5.0000 6.0000 5.0000 4.0000 4.0000 2.0000 2.0000
## Value_Index 15.3518 2.8394 -0.5185 0.3713 0.7784 0.4085 1.0397
## PseudoT2 Beale Ratkowsky Ball PtBiserial Frey McClain
## Number_clusters 2.0000 2.0000 2.0000 3.0000 3.0000 1 2.000
## Value_Index -0.6878 -0.0874 0.4466 18.8709 0.6361 NA 0.547
## Dunn Hubert SDindex Dindex SDbw
## Number_clusters 8.0000 0 4.0000 0 8.0000
## Value_Index 0.2509 0 1.2638 0 0.1636
(nb) + ()
## Among all indices:
## ===================
## * 2 proposed 0 as the best number of clusters
## * 1 proposed 1 as the best number of clusters
## * 8 proposed 2 as the best number of clusters
## * 2 proposed 3 as the best number of clusters
## * 4 proposed 4 as the best number of clusters
## * 5 proposed 5 as the best number of clusters
## * 1 proposed 6 as the best number of clusters
## * 3 proposed 8 as the best number of clusters
##
## Conclusion
## =========================
## * According to the majority rule, the best number of clusters is 2 .
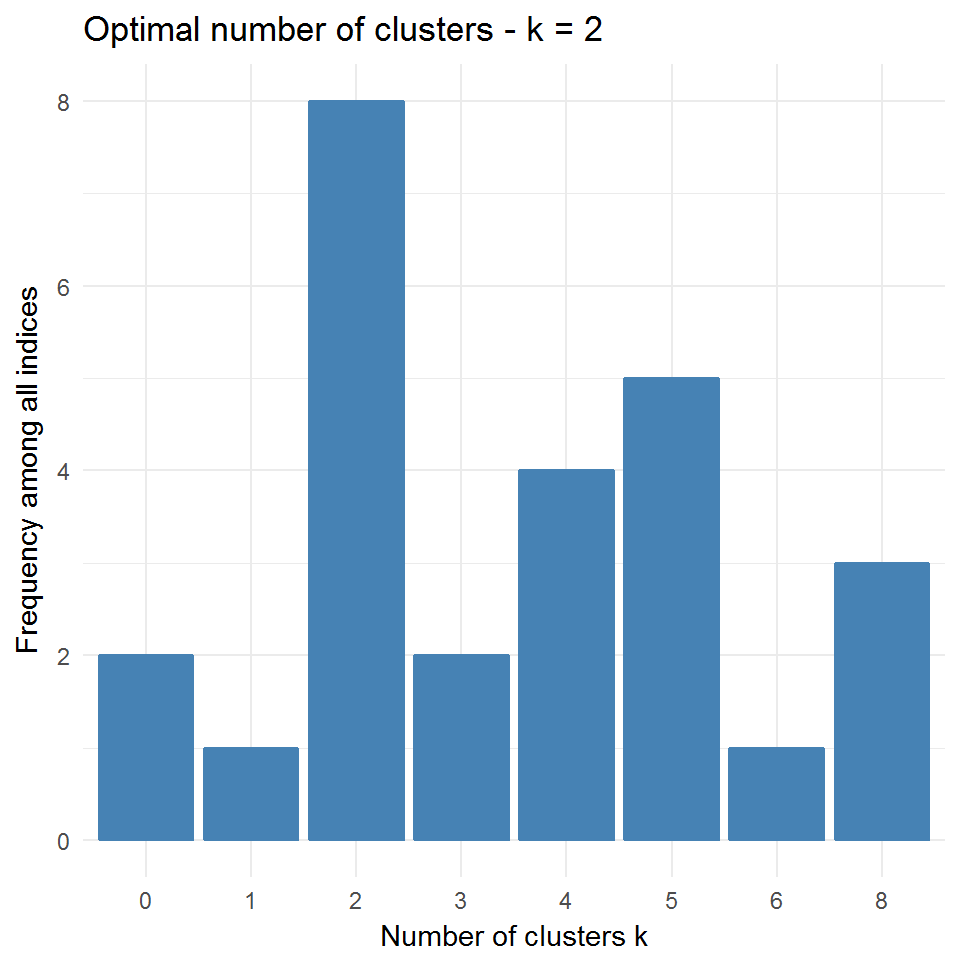
Рисунок 10.11: Оптимальное число кластеров по оценкам различных индексов
Разброс оценок числа классов наилучшего разбиения весьма велик: от 2 по индексу МакКлайна до 8 по индексу Данна, поэтому приходится прибегать к тривиальному голосованию.
Кофенетическую корреляцию можно также рассчитать между исходной матрицей дистанции и матрицей кофенетических расстояний, и тогда она может служить мерой адекватности кластерного решения исходным данным. Оценим по этому показателю пять иерархических кластеризаций, сравниваемых между собой в предыдущем разделе (Borcard et al., 2011):
d <- (df.stand, )
(vegan)
hc_list <- (hc1 <- (d,),
hc2 <- (d,), hc3 <- (d,),
hc4 <- (d, ), hc5 <- (d, ))
Coph <- (
MantelStat <- ((hc_list,
function(hc) (d, (hc))$statistic)),
MantelP <- ((hc_list,
function(hc) (d, (hc))$signif)))
(Coph) <- (, , , , )
(Coph) <- (, )
(Coph, )
## Complete Single Average Centroid Ward.D2
## W Мантеля 0.698 0.541 0.718 0.607 0.698
## Р-значение 0.001 0.001 0.001 0.001 0.001
Таким образом, максимальное значение коэффициента W матричной корреляции Мантеля (а, следовательно, и наибольшая адекватность матрице расстояний, построенной по исходным данным) принадлежит кластеризации по методу средней связи. Нелишне заметить, что все рассмотренные кластеризации статистически значимы, т.е. не могут быть объяснены случайными причинами (впрочем, такое будет почти всегда). Наконец, Ким и др. (1989) не рекомендуют использовать кофенетическую корреляцию в основном по причине несоответствия кофенетических расстояний нормальному распределению. Можно, однако, привести массу аргументов, показывающих откровенную слабость этих утверждений.
После того, как мы попытались оценить, насколько хорошо топология дендрограммы отображает предрасположенность объектов к группированию, остаются некоторые вопросы, вызывающие несомненный интерес. Можно ли вычислить -значения в целом для полученной иерархической кластеризации? Какие фрагменты древовидной структуры являются “слабым звеном” в полученной конструкции?
Однако правомерен и контрвопрос: “Нужно ли вычислять эти -значения?” Как убедительно сказано в книге Джеймс и др. (2016), не существует правильных или неправильных результатов кластеризации, поскольку, по определению, это метод обучения без учителя. Все определяется соответствием полученного решения поставленной задаче, которая на практике в большинстве случаев сводится просто к тому, чтобы приблизительно оценить, на сколько групп целесообразно разделить данные. При этом степень этого соответствия всегда будет субъективной.
Ответ на второй вопрос об устойчивости фрагментов кластерной структуры состоит в том, чтобы взять из исходной таблицы множество повторных выборок, построить для каждой из них свою дендрограмму и вычислить частоту встречаемости каждого фрагмента в сформированной последовательности разбиений. Разумеется, здесь невозможно обойтись без бутстрепа, позволяющего подсчитать вероятность BP (Bootstrap Probability) встречаемости произвольного узла в бутстреп-копиях. Обычно фрагменты древовидной структуры считаются статистически значимыми, если с ветвями дерева связывается бутстреп-вероятность, превышающая 70-80%.
Х. Шимодейра (Shimodaira, 2002), сравнивая центры распределения исходной и бутстреп-выборок, показал, что величина BP является приближенной оценкой вероятности появления узла в дереве. Несмещенную оценку вероятности AU (Approximately Unbiased) можно получить, выполнив повторную серию бутстрепа в различных масштабах (multiscale bootstrap resampling). Для этого отдельно вычисляют BP-значения, формируя бутстреп-выборки разного объема: например, (0.5n, 0.6n, dots, 1.4n, 1.5n), где – объем исходной выборки. Несмещенная бутстреп-вероятность AU находится аппроксимацией ряда полученных значений BP. Оптимальные оценки AU для каждого кластера дендрограммы, найденные путем подбора параметрических моделей с использованием метода максимального правдоподобия, могут быть получены с использованием пакетов pvclust и scaleboot для R.
Некоторая проблема заключается в том, что функция pvclust(), ориентированная на генетические исследования, выполняет кластеризацию признаков (т.е. столбцов таблицы данных), а для 4 показателей нашей демонстрационной таблицы USArrests это особого интереса не представляет. Если попробовать выполнить анализ с транспонированной матрицей (4 imes 60), выполнив команду pvclust(t(USArrests)), то решение найти нельзя из-за проблем с сингулярными преобразованиями:
Воспользуемся тогда в качестве примера набором Boston из пакета MASS, включающим 14 признаков привлекательности 506 участков города для проживания (рис. 10.12):
(Boston, )
(pvclust)
()
# Бутстреп деревьев и расчет BP- и AU- вероятностей для узлов
boston.pv <- (Boston, , ,
, )
(boston.pv) # дендрограмма с p-значениями
(boston.pv) # выделение боксами достоверных фрагментов
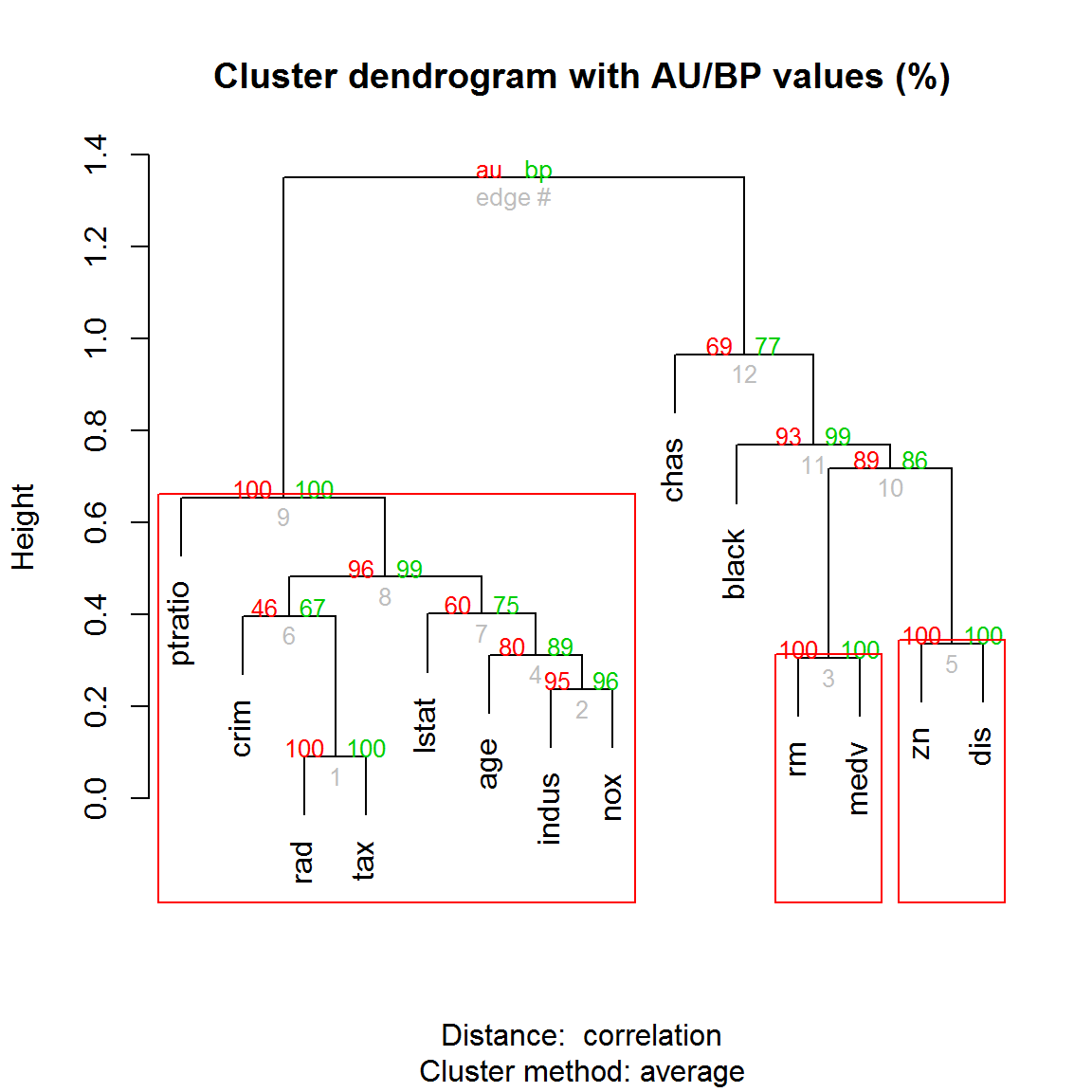
Рисунок 10.12: Дендрограмма с нанесенными значениями AU/BP для каждого узла
Этот пример показывает, что с практической точки зрения кластеризация признаков (переменных) может быть столь же важна, как и группировка объектов. Использование коэффициентов корреляции для расчета матрицы дистанций method.dist = “cor” избавляет нас от необходимости стандартизовать данные.
При анализе дендрограммы на рис. 10.12 можно увидеть, что признаки иногда образуют кластеры с ясно интерпретируемой зависимостью (“среднее число комнат в жилье rm” и “медианная стоимость дома medv”), но часто их тесная связь нуждается в дополнительном осмыслении (“индекс доступности к кольцевым дорогам rad” и “сумма налога на недвижимость tax”, или “доля участков, продаваемых в розницу indus” и “концентрация окислов азота nox”). В целом была получена весьма стабильная кластеризация: наименее низкую бутстреп-вероятность имеют такие важнейшие признаки, как “криминальный индекс crim” и “процент жителей с низким социальным статусом lstat”, которые вполне могут объединиться в группу с любым другим из имеющихся показателей (например, “долей афроамериканцев black”).

Рисунок 2.11 – Кластеризация агломеративным методом. Построение дендрограммы
1 Метод «ближних соседей» одиночной связи (Single Linkage). С его помощью можно связать два кластера вместе, когда два объекта в двух кластерах ближе друг к другу, чем соответствующее расстояние связи. Это правило строит «волокнистые» кластеры, «сцепленные вместе» только отдельными эле-

ментами, случайно оказавшимися ближе остальных друг к другу. Это правило нанизывает объекты вместе для формирования кластеров, и результирующие кластеры представляются длинными «цепочками».
2 Метод «дальних соседей» метод полной связи (Complete Linkage)
Как альтернативу первому способу можно использовать «соседей» в кластерах, которые находятся дальше всех остальных пар объектов друг от друга. Этот метод называется методом Он обычно работает очень хорошо, когда объекты происходят на самом деле из реально различных «рощ». Если же кластеры имеют удлиненную форму или их естественный тип «цепочечный», то этот метод непригоден.
3 Невзвешенное попарное среднее (Unweighted pair-group average).
этом методе расстояние между двумя различными кластерами вычисляют как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные «рощи», однако он работает одинаково хорошо и в случаях протяженных «цепочного» вида кластеров.
4 Взвешенное попарное среднее (Weighted pair-group average). Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях в качестве весового коэффициента используют размер соответствующих кластеров (число объектов, содержащихся в них). Данный метод следует использовать, когда предполагают неравные размеры кластеров.
5 Невзвешенный попарный центроидный метод (Unweighted pair-group centroid). В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести.
6 Взвешенный центроидный метод медиана (Weighted pair-group centroid). Этот метод идентичен предыдущему, за исключением того, что для учета разницы между размерами кластеров (то есть числами объектов в них) при вычислениях используют веса. Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего.
7 Метод Варда (Ward’s method). Этот метод отличается от всех других методов, поскольку он использует методы дисперсионного анализа для оценки расстояний между кластерами. Метод минимизирует сумму квадратов для любых двух (гипотетических) кластеров, которые могут быть сформированы на каждом шаге. Метод очень эффективен, однако он стремится создавать кластеры малого размера.
2.7 Пример проведения кластерного анализа алгоритмом древовидной кластеризации в пакетe STATISTICA 10

можно ли разделить претендентов на группы, и сколько таких групп может получиться исходя из результатов профотбора?
1 Таблица с исходными данными у нас уже имеется. Поэтому, как и в предыдущем примере стандартизируем данные, чтобы привести их к одному порядку по шкале от –1 до 1: из значений переменных вычтем их среднее, и эти значения поделим на стандартное отклонение. Во вкладке в группе выберем команду , и
Standardization of Values (Стандартизация значений) зададим значения параметров (рисунок 2.2):
– All (Все);
– Off (Не задавать). Нажав , выполним стандартизацию.
2 На вкладке Statistics (Анализ) Advanced/Multivariate (Углуб-
ленная статистика) Mult/Exploratory (Многомерный анализ) Cluster (Кластерный анализ)
3 В появившемся окне Clustering Method (Методы кластеризации)
нок 2.1) выберем метод Joining (tree clustering) (Иерархическая классифика-
и нажмем .
4 В диалоговом окне этого метода Cluster Analysis: Joining (Tree Clustering) (Кластерный анализ: иерархическая классификация) во вкладке
Advanced (Дополнительно) (рисунок 2.12) заполним:
Input file (Файл данных) Raw data (Исходные данные)
поскольку данные у нас уже имеются (можно открывать и ранее сохраненный файл);
зададим направление классификации – Cases (Rows) (Наблюдения (строки));
Amalgamation (linkage) rule (Правило объединения)
тановку для выбора различных мер сходства – Ward’s method (Метод Варда);
Distance measure (Мера близости) зададим метрику – Euclidean distances (Евклидово расстояние)
MD deletaion (Удаление пропущенных данных))
брать два способа некомплектных наблюдений, содержащих пропуски хотя бы одной переменной: – некомплектные наблюдения полностью исключаются их дальнейшего анализа; Mean substitution (Замена средним) – пропущенные данные заменяют срежними значениями показателя, полученным по комплектным (полным) данным – в данном примере выберем построчное удаление .
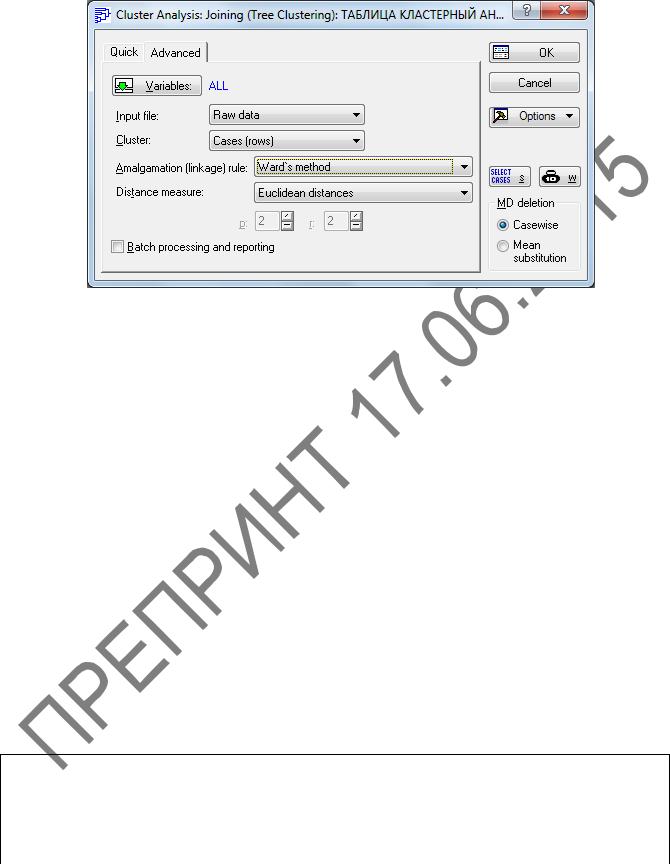
Рисунок 2.12 – Окно Cluster Analysis: Joining (Tree Clustering)
5 Нажав , выполним кластеризацию. В окне Joining Results (Результаты иерархической классификации) (рисунок 2.13) переходим на вкладку и нажимаем кнопку Vertical icicle plot (Вертикальная дендро-
. На появившейся дендрограмме (рисунок 2.14) горизонтальная ось представляет наблюдения, вертикальная – расстояние объединения. Дендрограмма показывает процесс объединения. На расстоянии, равном 4, существуют 4 кластера; на расстоянии, равном 7, существуют три кластера; при увеличении расстояния до 13 количество кластеров становится равным двум; на расстоянии, равном 23, остался один кластер.
Сравним результаты кластеризации по алгоритмам -средних и древовидной кластеризации для количества кластеров, равного 4 (таблицы 2.4 и 2.5). Содержимое первых и четвертых кластеров здесь совпадает, а в содержимом вторых и третьих кластеров наблюдаются небольшие отличия.
Таблица 2.5 – Результаты кластерного анализа по алгоритму иерархической классификации
Разбиение выборки на 4 кластера
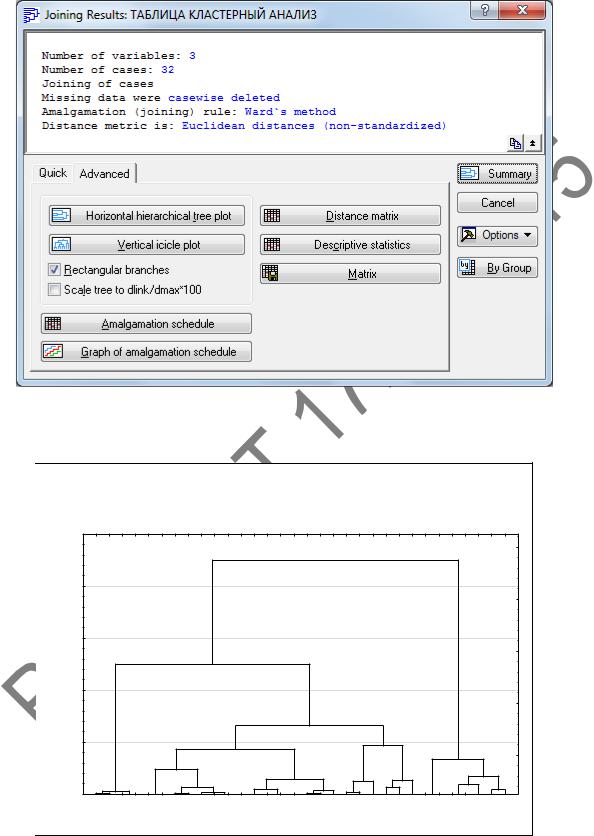
Рисунок 2.13 – Окно
Дендрограмма для 32 наблюдений Метод Варда
C_16 C_15 C_31 C_13 C_24 C_14 C_28 C_20 C_32 C_23 C_17 C_7 C_11 C_21 C_19 C_9 C_29 C_18 C_5 C_30 C_27 C_25 C_8 C_3 C_2 C_26 C_22 C_12 C_6 C_4 C_10 C_1
Рисунок 2.14 – Дендрограмма иерархической классификации
6 В окне Joining Results (Результаты иерархической классификации)
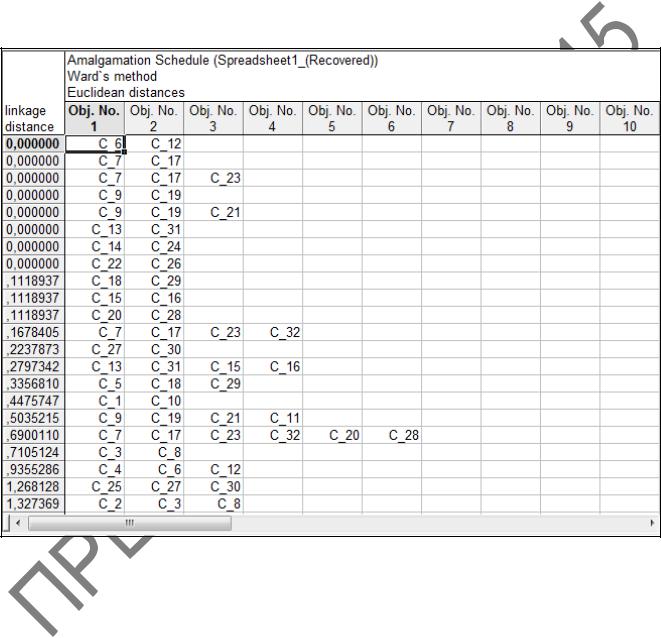
(рисунок 2.13) нажмем на кнопку Amalgamation schedule (Схема объединения) и выведем на экран таблицу результатов со схемой объединения (рисунок 2.15). Первый столбец таблицы содержит расстояния до соответствующих кластеров. Каждая строка показывает состав кластера на данном шаге классификации. Например, на первом шаге (1 строка) объединяются наблюдения 6 и 12, на втором (2 строка) – 7 и 17, на третьем (3 строка) – 7, 17 и 23 и так далее. Закончилось объединение на расстоянии 22,4. Закроим таблицу.
Рисунок 2.15 – Схема объединения
7 В окне Joining Results (Результаты иерархической классификации)
(рисунок 2.13) нажмем на кнопку Graph of amalgamation schedule (График схе-
и просмотрим результаты древовидной кластеризации (рисунок 2.16). По горизонтальной оси на диаграмме отложены шаги, по вертикальной – расстояния. Всего алгоритму потребовалось 31 шаг для объединения всех объектов в один кластер. Закроим график.
8 В окне Joining Results (Результаты иерархической классификации)
(рисунок 2.13) нажмем на кнопку Distance matrix (Матрица расстояний) и про-
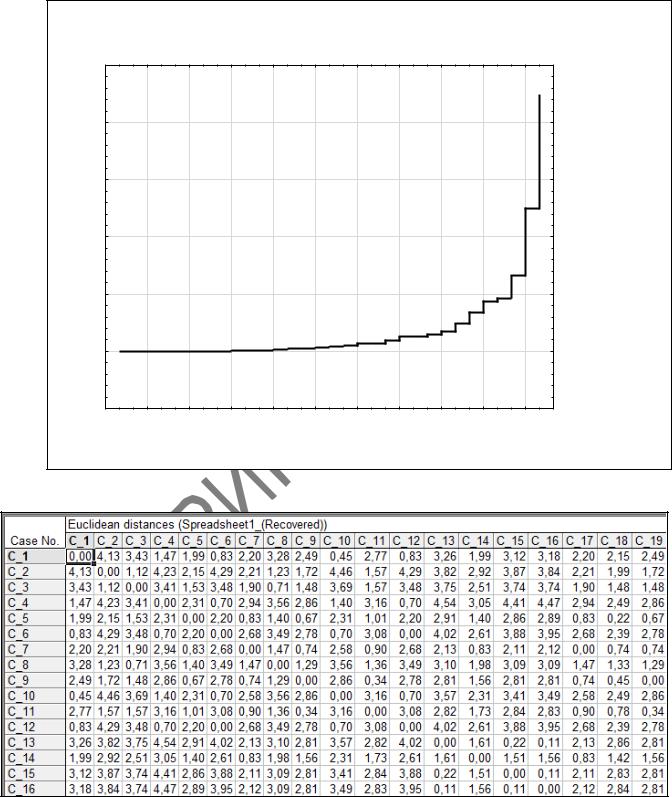
смотрим матрицу Евклидовых расстояний между различными наблюдениями (ри-
Диаграмма расстояний объединения по шагам Евклидово расстояние
Рисунок 2.16 – График схемы объединения
Рисунок 2.17 – Матрица Евклидовых расстояний между различными наблюдениями

2.8 Проблемы алгоритмов кластеризации
Одно и то же множество наблюдений можно разбить на несколько кластеров по-разному. Это приводит к изобилию алгоритмов кластеризации.
При решении задач кластеризации популярны алгоритмы, которые ищут оптимальное разбиение множества данных на группы. Критерий оптимальности определяется видом целевой функции, от которой зависит результат кластеризации.
Например, семейство алгоритмов –
средних показывает хорошие результаты, когда данные в пространстве образуют компактные сгустки, четко отличимые друг от друга. Поэтому и критерий качества основан
На рисунке 2.18 приведен пример неуспеха алгоритма -средних. При использовании Евклидовой метрики кластеры в – средних имеют сферическую форму, поэтому такой алгоритм никогда не разделит на кластеры вложенные друг в друга множества объектов.
1 Двух или трех кластеров, как правило, недостаточно: кластеризация будет слишком грубой, приводящей к потере информации об индивидуальных свойствах объектов.
2 Больше десяти кластеров не укладываются в «число Миллера 7 ± 2»: аналитику трудно держать в кратковременной памяти столько кластеров. Поэтому в подавляющем большинстве случаев число кластеров варьируется от 4 до 9.
Чтобы применять кластеризацию корректно и снизить риск получения результатов, не имеющих отношения к действительности, необходимо придерживаться следующих правил:

1 Перед кластеризацией четко обозначьте цели еѐ проведения: облегчение дальнейшего анализа, сжатие данных и тому подобно. Кластеризация сама по себе не представляет особой ценности.
2 Выбирая алгоритм, убедитесь, что он корректно работает с теми данными, которыми вы располагаете для кластеризации. В частности, если присутствуют категориальные признаки, удостоверьтесь, что та реализация алгоритма, которую вы используете, умеет правильно обрабатывать их. Это особенно актуально для алгоритма -средних, применяющего Евклидову меру расстояния. Если алгоритм не умеет работать со смешанными наборами данных, постарайтесь сделать набор данных однородным, то есть отказаться от категориальных или числовых признаков.
3 Обязательно проведите содержательную интерпретацию каждого полученного кластера: постарайтесь понять, почему объекты были сгруппированы в определенный кластер, что их объединяет. Полезно каждому кластеру дать емкое название, состоящее из нескольких слов. Встречаются ситуации, когда алгоритм кластеризации не выделил никаких особых групп. Возможно, набор данных и до кластеризации был однороден, не расслаивался на изолированные подмножества, а кластеризация подтвердила эту гипотезу.
Таким образом, не существует единого универсального алгоритма кластеризации. При использовании любого алгоритма важно понимать его достоинства, недостатки и ограничения. Только тогда кластеризация будет эффективным инструментом в руках аналитика.
2.9 Варианты заданий по кластерному анализу в пакете STATISTICA 10
Для всех вариантов заданий произвести следующий анализ: 1 Стандартизировать исходные данные.
2 Произвести кластерный анализ таблицы алгоритмом средних для числа кластеров 3, 4 и 5. Получить описательные статистики для каждого кластера. Определить центроиды для каждого кластера и Евклидово расстояние между кластерами. Построить графики средних для каждого кластера. Выбрать оптимальное количество кластеров по величинам межгрупповой и внутригрупповой дисперсий.
3 Произвести кластерный анализ алгоритмом древовидной классификации, используя различные правила объединения (метод «ближайших соседей», метод «дальних соседей», невзвешенное попарное среднее, взвешенное попарное среднее, невзвешенный попарный центроидный метод, взвешенный центороидный метод, метод Варда) и метрики пространства (Евклидово расстояние, расстояние Манхеттена, расстояние Чебышева, степенное расстояние). Построить дендрограммы иерархической классификации, схемы объединения, графики схем объединения и матрицы расстояний между наблюдениями. Сравнить результаты кластеризации, полученные с помощью различных правил объединения и метрик пространства.

4 Сравнить результаты кластеризации алгоритмами средних и древовидной классификации. Сделать выводы.
Имеются результаты измерения спортивных показателей 1, 2, 3, 4, 5 женщин-спортсменок в количестве 40 человек (таблица 2.6).
Очень
важным вопросом является проблема
выбора необходимого числа кластеров.
Иногда можно m
число кластеров выбирать априорно.
Однако в общем случае это число
определяется в процессе разбиения
множества на кластеры.
Проводились
исследования Фортьером и Соломоном, и
было установлено, что число кластеров
должно быть принято для достижения
вероятности
того, что найдено наилучшее разбиение.
Таким образом, оптимальное число
разбиений является функцией заданной
доли
наилучших или в некотором смысле
допустимых разбиений во множестве всех
возможных. Общее рассеяние будет тем
больше, чем выше доля
допустимых разбиений. Фортьер и Соломон
разработали таблицу, по которой можно
найти число необходимых разбиений.
S(
в зависимости от
и
(где
– вероятность того, что найдено наилучшее
разбиение,
– доля
наилучших разбиений в общем числе
разбиений) Причем в качестве меры
разнородности используется не мера
рассеяния, а мера принадлежности,
введенная Хользенгером и Харманом.
Таблица значений S(
)
приводится
ниже.
Довольно
часто критерием объединения (числа
кластеров) становится изменение
соответствующей функции. Например,
суммы квадратов отклонений:
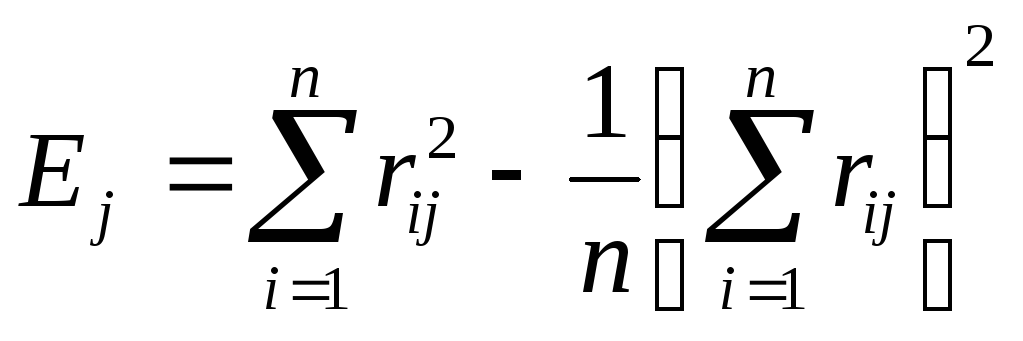
Процессу
группировки должно соответствовать
здесь последовательное минимальное
возрастание значения критерия E.
Наличие резкого скачка в значении E
можно интерпретировать как характеристику
числа кластеров, объективно существующих
в исследуемой совокупности.
Итак, второй способ
определения наилучшего числа кластеров
сводится к выявлению скачков, определяемых
фазовым переходом от сильно связанного
к слабосвязанному состоянию объектов.
6 Дендограммы.
Наиболее известный
метод представления матрицы расстояний
или сходства основан на идее дендограммы
или диаграммы дерева. Дендограмму можно
определить как графическое изображение
результатов процесса последовательной
кластеризации, которая осуществляется
в терминах матрицы расстояний. С помощью
дендограммы можно графически или
геометрически изобразить процедуру
кластеризации при условии, что эта
процедура оперирует только с элементами
матрицы расстояний или сходства.
Существует много
способов построения дендограмм. В
дендограмме объекты располагаются
вертикально слева, результаты
кластеризации – справа. Значения
расстояний или сходства, отвечающие
строению новых кластеров, изображаются
по горизонтальной прямой поверх
дендограмм.
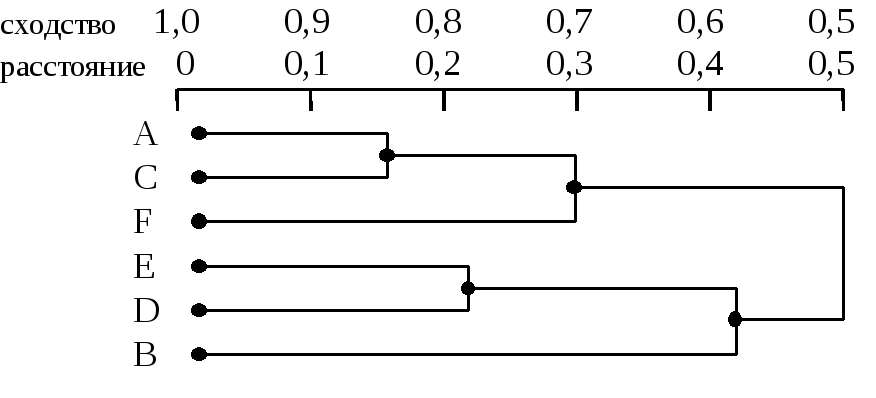
На
рисунке 1 показан один из примеров
дендограммы. Рис 1 соответствует случаю
шести объектов (n=6)
и k
характеристик (признаков). Объекты А
и С
наиболее близки и поэтому объединяются
в один кластер на уровне близости, равном
0,9. Объекты D
и Е
объединяются при уровне 0,8. Теперь имеем
4 кластера:
(А,
С), (F),
(D,
E), (B).
Далее
образуются кластеры (А,
С, F)
и (E,
D, B),
соответствующие уровню близости, равному
0,7 и 0,6. Окончательно все объекты
группируются в один кластер при уровне
0,5.
Вид дендограммы
зависит от выбора меры сходства или
расстояния между объектом и кластером
и метода кластеризации. Наиболее важным
моментом является выбор меры сходства
или меры расстояния между объектом и
кластером.
Число алгоритмов
кластерного анализа слишком велико.
Все их можно подразделить на иерархические
и неиерархические.
Иерархические
алгоритмы связаны с построением
дендограмм и делятся на:
а) агломеративные,
характеризуемые последовательным
объединением исходных элементов и
соответствующим уменьшением числа
кластеров;
б) дивизимные
(делимые), в которых число кластеров
возрастает, начиная с одного, в результате
чего образуется последовательность
расщепляющих групп.
Алгоритмы кластерного
анализа имеют сегодня хорошую программную
реализацию, которая позволяет решить
задачи самой большой размерности.
Кластеризация неразмеченных данных можно выполнить с помощью модуля sklearn.cluster.
Каждый алгоритм кластеризации имеет два варианта: класс, реализующий fit метод изучения кластеров на данных поезда, и функция, которая, учитывая данные поезда, возвращает массив целочисленных меток, соответствующих различным кластерам. Для класса метки над обучающими данными можно найти в labels_ атрибуте.
Обзор методов кластеризации
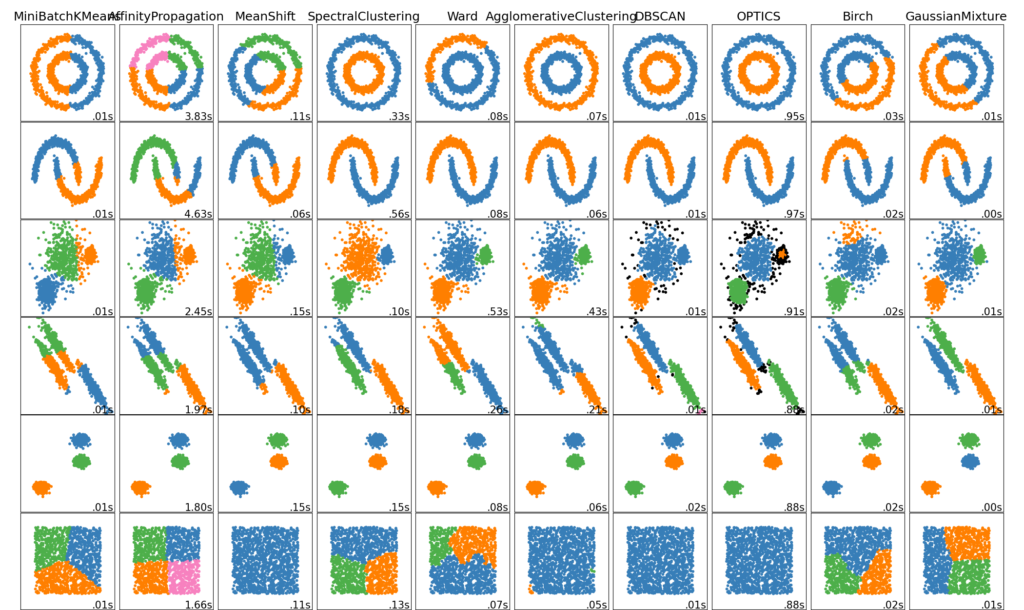
Неплоская геометрия кластеризации полезно когда кластеры имеют специфичную форму, то есть многообразие и стандартное евклидовое расстояние в качестве метрики не подходят. Это случай возникает в двух верхних строках рисунка.
Гауссовская Смешаянная модель полезна для кластеризации описанные в другой статье документации, посвященная смешанным моделям. Метод K-средних можно расматривать как частный случай Гауссовской смешанной модели с равной ковариации для каждого компонента.
Методы трансдуктивной кластеризации (в отличие отметодов индуктивной кластеризации) не предназначены для применения к новым, невидимым данным.
K-средних
Эти KMeans данные алгоритмы кластеров пытаются отдельными образцы в п групп одинаковой дисперсии, сводя к минимуму критерия , известный как инерция или внутри-кластера сумм квадратов (см ниже). Этот алгоритм требует указания количества кластеров. Он хорошо масштабируется для большого количества образцов и используется в широком диапазоне областей применения во многих различных областях.
Алгоритм k-средних делит набор $N$ образцы $X$ в $K$ непересекающиеся кластеры $C$, каждый из которых описывается средним $mu_j$ образцов в кластере. Средние значения обычно называют «центроидами» кластера; обратите внимание, что это, как правило, не баллы из $X$, хотя они живут в одном пространстве.
Инерцию можно определить как меру того, насколько кластеры внутренне связаны. Он страдает различными недостатками:
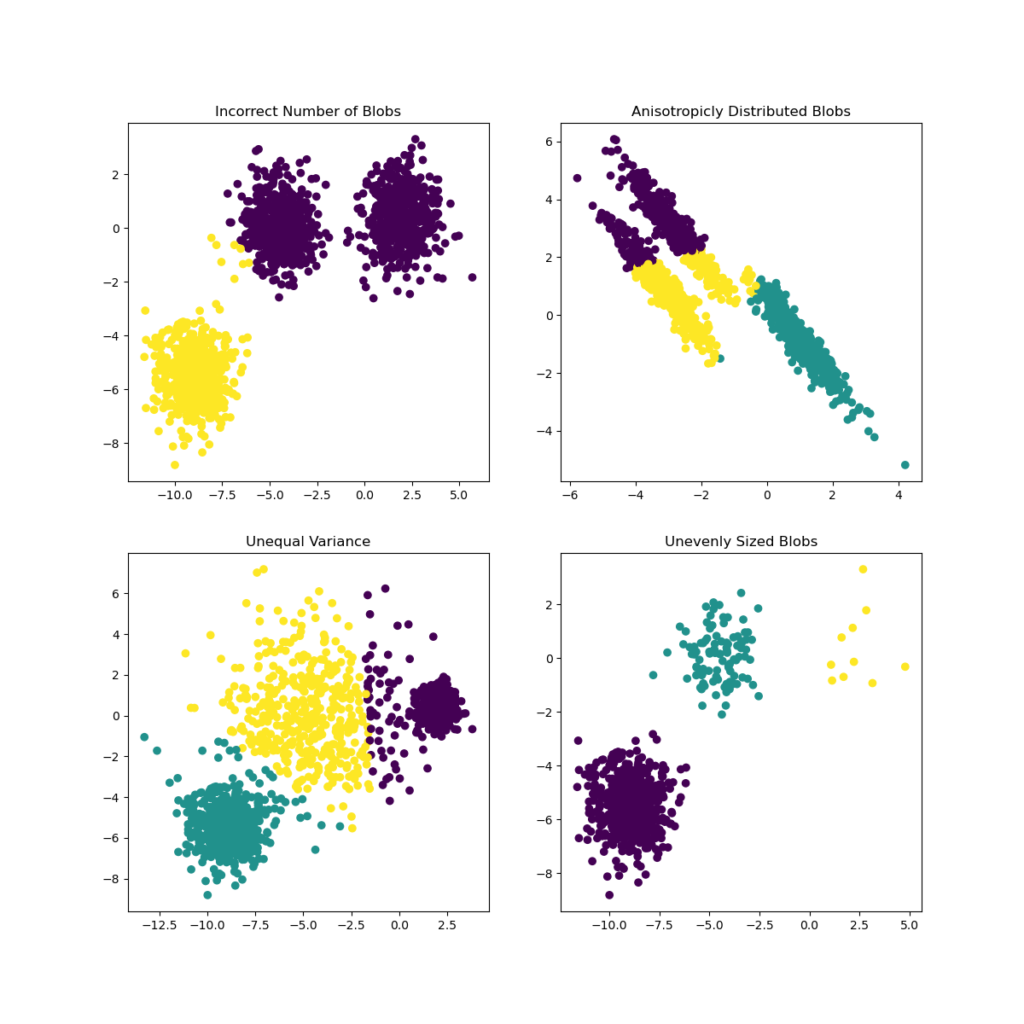
- Инерция предполагает, что кластеры выпуклые и изотропные, что не всегда так. Он плохо реагирует на удлиненные кластеры или коллекторы неправильной формы.
- Инерция — это не нормализованная метрика: мы просто знаем, что более низкие значения лучше, а ноль — оптимально. Но в очень многомерных пространствах евклидовы расстояния имеют тенденцию становиться раздутыми (это пример так называемого «проклятия размерности»). Выполнение алгоритма уменьшения размерности, такого как анализ главных компонентов (PCA) перед кластеризацией k-средних, может облегчить эту проблему и ускорить вычисления.
K-средних часто называют алгоритмом Ллойда. В общих чертах алгоритм состоит из трех шагов. На первом этапе выбираются начальные центроиды, а самый простой метод — выбрать $k$ образцы из набора данных $X$. После инициализации K-средних состоит из цикла между двумя другими шагами. Первый шаг присваивает каждой выборке ближайший центроид. На втором этапе создаются новые центроиды, взяв среднее значение всех выборок, назначенных каждому предыдущему центроиду. Вычисляется разница между старым и новым центроидами, и алгоритм повторяет эти последние два шага, пока это значение не станет меньше порогового значения. Другими словами, это повторяется до тех пор, пока центроиды не переместятся значительно.
K-средних эквивалентно алгоритму максимизации ожидания с маленькой, все равной диагональной ковариационной матрицей.
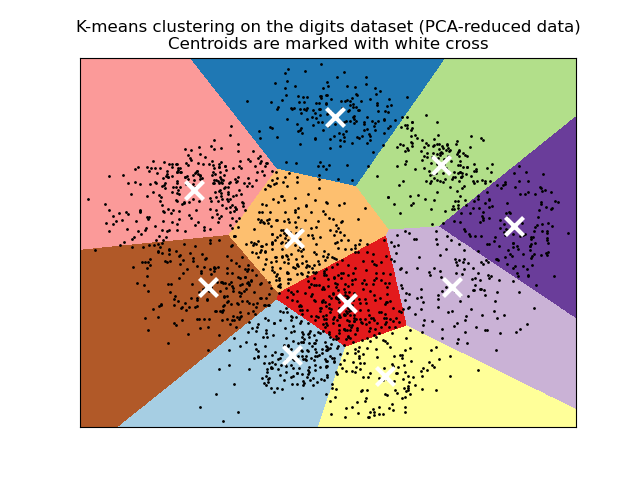
Алгоритм также можно понять через концепцию диаграмм Вороного. Сначала рассчитывается диаграмма Вороного точек с использованием текущих центроидов. Каждый сегмент на диаграмме Вороного становится отдельным кластером. Во-вторых, центроиды обновляются до среднего значения каждого сегмента. Затем алгоритм повторяет это до тех пор, пока не будет выполнен критерий остановки. Обычно алгоритм останавливается, когда относительное уменьшение целевой функции между итерациями меньше заданного значения допуска. В этой реализации дело обстоит иначе: итерация останавливается, когда центроиды перемещаются меньше допуска.
По прошествии достаточного времени K-средние всегда будут сходиться, однако это может быть локальным минимумом. Это сильно зависит от инициализации центроидов. В результате вычисление часто выполняется несколько раз с разными инициализациями центроидов. Одним из способов решения этой проблемы является схема инициализации k-means++, которая была реализована в scikit-learn (используйте init=’k-means++’параметр). Это инициализирует центроиды (как правило) удаленными друг от друга, что, вероятно, приводит к лучшим результатам, чем случайная инициализация, как показано в справочнике.
K-means++ также может вызываться независимо для выбора начальных значений для других алгоритмов кластеризации, sklearn.cluster.kmeans_plusplus подробности и примеры использования см. В разделе .
Алгоритм поддерживает выборочные веса, которые могут быть заданы параметром sample_weight. Это позволяет присвоить некоторым выборкам больший вес при вычислении центров кластеров и значений инерции. Например, присвоение веса 2 выборке эквивалентно добавлению дубликата этой выборки в набор данных $X$.
Метод K-средних может использоваться для векторного квантования. Это достигается с помощью метода преобразования обученной модели KMeans.
Низкоуровневый параллелизм
KMeans преимущества параллелизма на основе OpenMP через Cython. Небольшие порции данных (256 выборок) обрабатываются параллельно, что, кроме того, снижает объем памяти. Дополнительные сведения о том, как контролировать количество потоков, см. В наших заметках о параллелизме .
Мини-партия K-средних
Это MiniBatchKMeans вариант KMeans алгоритма, который использует мини-пакеты для сокращения времени вычислений, но при этом пытается оптимизировать ту же целевую функцию. Мини-пакеты — это подмножества входных данных, которые выбираются случайным образом на каждой итерации обучения. Эти мини-пакеты резко сокращают объем вычислений, необходимых для схождения к локальному решению. В отличие от других алгоритмов, которые сокращают время сходимости k-средних, мини-пакетные k-средние дают результаты, которые, как правило, лишь немного хуже, чем стандартный алгоритм.
Алгоритм повторяется между двумя основными шагами, аналогично обычным k-средним. На первом этапе $b$ образцы выбираются случайным образом из набора данных, чтобы сформировать мини-пакет. Затем они присваиваются ближайшему центроиду. На втором этапе обновляются центроиды. В отличие от k-средних, это делается для каждой выборки. Для каждой выборки в мини-пакете назначенный центроид обновляется путем взятия среднего потокового значения выборки и всех предыдущих выборок, назначенных этому центроиду. Это приводит к снижению скорости изменения центроида с течением времени. Эти шаги выполняются до тех пор, пока не будет достигнута сходимость или заранее определенное количество итераций.
MiniBatchKMeans сходится быстрее, чем KMeans, но качество результатов снижается. На практике эта разница в качестве может быть довольно небольшой, как показано в примере и цитированной ссылке.
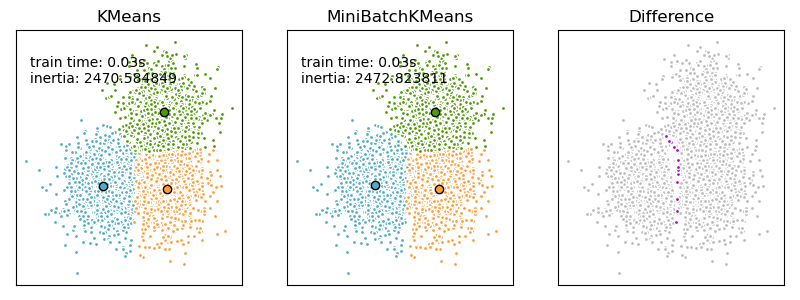
Распространения близости (Affinity Propagation)
AffinityPropagation создает кластеры, отправляя сообщения между парами образцов до схождения. Затем набор данных описывается с использованием небольшого количества образцов, которые определяются как наиболее репрезентативные для других образцов. Сообщения, отправляемые между парами, представляют пригодность одного образца быть образцом другого, который обновляется в ответ на значения из других пар. Это обновление происходит итеративно до сходимости, после чего выбираются окончательные образцы и, следовательно, дается окончательная кластеризация.
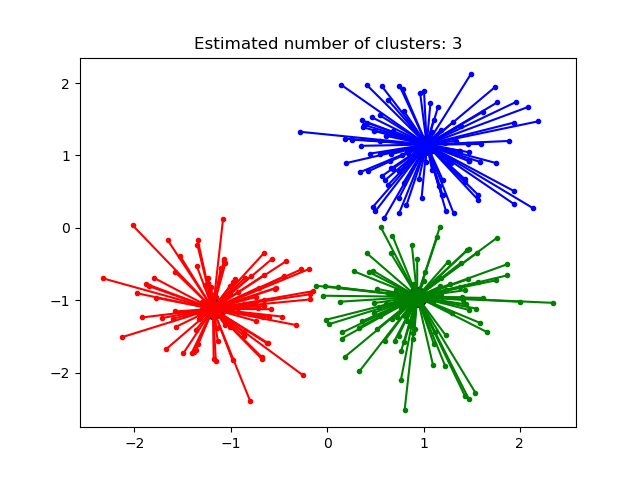
Метод Распространения близости может быть интересным, поскольку он выбирает количество кластеров на основе предоставленных данных. Для этой цели двумя важными параметрами являются предпочтение , которое контролирует, сколько экземпляров используется, и коэффициент демпфирования, который снижает ответственность и сообщения о доступности, чтобы избежать числовых колебаний при обновлении этих сообщений.
Главный недостаток метода Распространения близости — его сложность. Алгоритм имеет временную сложность порядка $O(N^2 T)$, где $N$ количество образцов и $T$ — количество итераций до сходимости. Далее, сложность памяти порядка $O(N^2)$ если используется плотная матрица подобия, но может быть сокращена, если используется разреженная матрица подобия. Это делает метод Распространения близости наиболее подходящим для наборов данных малого и среднего размера.
Описание алгоритма: сообщения, отправляемые между точками, относятся к одной из двух категорий. Во-первых, это ответственность $r(i,k)$, которое является накопленным свидетельством того, что образец $k$ должен быть образцом для образца $i$. Второе — доступность $a(i,k)$ что является накопленным свидетельством того, что образец $i$ следует выбрать образец $k$ быть его образцом, и учитывает значения для всех других образцов, которые $k$ должен быть образцом. Таким образом, образцы выбираются по образцам, если они (1) достаточно похожи на многие образцы и (2) выбираются многими образцами, чтобы быть репрезентативными.
где $t$ указывает время итерации.
Средний сдвиг
MeanShift кластеризация направлена на обнаружение капель в образцах с плавной плотностью. Это алгоритм на основе центроидов, который работает, обновляя кандидатов в центроиды, чтобы они были средними точками в данном регионе. Затем эти кандидаты фильтруются на этапе постобработки, чтобы исключить почти дубликаты и сформировать окончательный набор центроидов.
Алгоритм автоматически устанавливает количество кластеров, вместо того, чтобы полагаться на параметр bandwidth, который определяет размер области для поиска. Этот параметр можно установить вручную, но можно оценить с помощью предоставленной estimate_bandwidth функции, которая вызывается, если полоса пропускания не задана.
Алгоритм не отличается высокой масштабируемостью, так как он требует многократного поиска ближайшего соседа во время выполнения алгоритма. Алгоритм гарантированно сходится, однако алгоритм прекратит итерацию, когда изменение центроидов будет небольшим.
Маркировка нового образца выполняется путем нахождения ближайшего центроида для данного образца.
Спектральная кластеризация
SpectralClustering выполняет низкоразмерное встраивание матрицы аффинности между выборками с последующей кластеризацией, например, с помощью K-средних, компонентов собственных векторов в низкоразмерном пространстве. Это особенно эффективно с точки зрения вычислений, если матрица аффинности является разреженной, а amgрешатель используется для проблемы собственных значений (обратите внимание, amg что решающая программа требует, чтобы был установлен модуль pyamg ).
Текущая версия SpectralClustering требует, чтобы количество кластеров было указано заранее. Это хорошо работает для небольшого количества кластеров, но не рекомендуется для многих кластеров.
Для двух кластеров SpectralClustering решает выпуклую релаксацию проблемы нормализованных разрезов на графе подобия: разрезание графа пополам так, чтобы вес разрезаемых рёбер был мал по сравнению с весами рёбер внутри каждого кластера. Этот критерий особенно интересен при работе с изображениями, где вершинами графа являются пиксели, а веса ребер графа подобия вычисляются с использованием функции градиента изображения.
Преобразование расстояния в хорошее сходство
Обратите внимание, что если значения вашей матрицы подобия плохо распределены, например, с отрицательными значениями или с матрицей расстояний, а не с подобием, спектральная проблема будет сингулярной, а проблема неразрешима. В этом случае рекомендуется применить преобразование к элементам матрицы. Например, в случае матрицы расстояний со знаком обычно применяется тепловое ядро:
similarity = np.exp(-beta * distance / distance.std())
См. Примеры такого приложения.
Различные стратегии присвоения меток
Могут использоваться различные стратегии присвоения меток, соответствующие assign_labels параметру SpectralClustering. “kmeans” стратегия может соответствовать более тонким деталям, но может быть нестабильной. В частности, если вы не контролируете random_state, он может не воспроизводиться от запуска к запуску, так как это зависит от случайной инициализации. Альтернативная “discretize” стратегия воспроизводима на 100%, но имеет тенденцию создавать участки довольно ровной и геометрической формы.