Карточки-задания для самостоятельной работы геометрии на тему “Вписаные и описанные многоугольники”, 10 класс

Определение четырехугольника, вписанного в окружность.

Около какого четырехугольника можно описать окружность.

4.Свойство противолежащих сторон
описанного четырехугольника.

5. Можно ли около ромба описать окружность.

6. Среди приведенных четырехугольников
укажите четырехугольник, который может быть вписан в окружность, но не может
быть описан около нее

7. Найдите углы
вписанного четырехугольника, если два его угла равны 110° и 100°

Определение четырехугольника, описанного около окружности.

Чему равна сумма противолежащих углов вписанного
четырехугольника.

При каком условии в четырехугольник можно вписать окружность.

Свойство трапеции, вписанной в четырехугольник.

Можно ли около параллелограмма описать окружность.

6. Среди приведенных четырехугольников
укажите четырехугольник, который может быть описан около окружности, но не
может быть вписан в нее

Найти сторону описанного около окружности четырехугольника, три
последовательные стороны которого равны 5см, 7см, 5см.

Самостоятельные работы по геометрии в 8 классе с ответами и решениями для УМК Атанасян и др. (3 уровня сложности по 2 варианта). В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 8 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение». Геометрия 8 класс Самостоятельные работы.

Геометрия 8 класс Самостоятельные работы
к УМК Л. Атанасяна и др.

1) к Уроку 4. Решение задач по теме «Многоугольники».

Самостоятельная работа № 1 + Ответы

2) к Уроку 7. Решение задач по теме «Параллелограмм».

Самостоятельная работа № 2 + Ответы

3) к Уроку 9. Теорема Фалеса.

4) к Уроку 13. Решение задач по теме «Прямоугольник. Ромб. Квадрат».

к Уроку 14. Осевая и центральная симметрии.

ГЛАВА VI. ПЛОЩАДЬ

5) к Уроку 18. Площадь прямоугольника.

6) к Уроку 21. Площадь треугольника.

7) к Уроку 24. Решение задач на вычисление площади.

8) к Уроку 27. Решение задач по теме «Теорема Пифагора»

Самостоятельная работа № 8 + Ответы

ГЛАВА VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

9) к Уроку 36. Решение задач на применение признаков подобия треугольников.

Самостоятельная работа № 9 + Ответы

10) к Уроку 40. Средняя линия треугольника. Свойство медиан треугольника

Самостоятельная работа № 10 + Ответы

11) к Уроку 42. Пропорциональные отрезки в прямоугольном треугольнике

Самостоятельная работа № 11 + Ответы

12) к Уроку 48. Решение задач по теме «Соотношения между сторонами и углами прямоугольного треугольника».

Самостоятельная работа № 12 + Ответы

ГЛАВА VIII. ОКРУЖНОСТЬ

13) Урок 53. Решение задач по теме «Касательная к окружности».

Самостоятельная работа № 13 + Ответы

14) Урок 57. Решение задач по теме «Центральные и вписанные углы»

Самостоятельная работа № 14 + Ответы

15) Урок 62. Свойство описанного четырехугольника.

Самостоятельная работа № 15 + Ответы

16) Урок 64. Свойство вписанного четырехугольника.

Самостоятельная работа № 16 + Ответы

При прохождении каждой темы предусмотрено 4 самостоятельные работы, состоящие из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы. Варианты 1, 2 — самые простые, варианты 3, 4 — сложнее и варианты 5, 6 — самые сложные). При этом сложность вариантов нарастает не очень резко.

Вы смотрели: Самостоятельные работы по геометрии в 8 классе с ответами и решениями для УМК Атанасян и др. (3 уровня сложности по 2 варианта). В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 8 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение». Геометрия 8 класс Самостоятельные работы.

Вернуться к Списку уроков Тематического планирования в 8 классе.

Самостоятельная работа № 15 по геометрии в 8 классе с ответами (3 уровня сложности по 2 варианта). Урок 62. «Свойство описанного четырехугольника» УМК Атанасян и др. (Просвещение). Геометрия 8 класс Самостоятельная 15. Поурочное планирование по геометрии.

Смотреть Список самостоятельных работ по геометрии в 8 классе.

Основная дидактическая цель урока: совершенствовать навыки решения задач.
Тип урока: урок контроля, оценки и коррекции знаний.

Организационный момент

Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.

Выполнение работы «Свойство описанного четырехугольника»

II уровень сложности

Рефлексия учебной деятельности

В конце урока учитель раздает на каждую парту краткую запись решения задач самостоятельной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.

Ответы на самостоятельную работу
I уровня сложности

С–15. 1 ур. Вариант 1

№ 1. В равносторонний треугольник вписана окружность радиусом 4 см. Найдите сторону треугольника.
ОТВЕТ: 8√3 см.

№ 2. Четырехугольник ABCD описан около окружности. Найдите стороны АВ и CD, если ВС = 6 см, AD = 9 см, АВ в 2 раза больше, чем CD.
ОТВЕТ: АВ = 10 см, CD = 5 см.

С–15. 1 ур. Вариант 2

№ 1. В равносторонний треугольник со стороной 8 см вписана окружность. Найдите радиус окружности.
ОТВЕТ: (4√3)/3 см.

№ 2. Четырехугольник ABCD описан около окружности. Найдите стороны ВС и AD, если АВ = 7 см, CD = 11 см, ВС в 2 раза меньше AD.
ОТВЕТ: ВС = 6 см, AD = 12 см.

Ответы на самостоятельную работу
II уровня сложности

С–15. 2 ур. Вариант 1

№ 1. В прямоугольном треугольнике ABC (∠C = 90°) АВ = 10 см, радиус вписанной в него окружности равен 2 см. Найдите площадь этого треугольника.
ОТВЕТ: 24 см2.

№ 2. В равнобедренной трапеции разность оснований равна 20 см, а радиус вписанной в нее окружности равен 2√14 см. Найдите стороны трапеции.
ОТВЕТ: 8, 18, 24, 18 см.

С–15. 2 ур. Вариант 2

№ 1. В прямоугольном треугольнике ABC (∠C = 90°) АС + ВС = 17 см, радиус вписанной в него окружности равен 2 см. Найдите площадь этого треугольника.
ОТВЕТ: 30 см2.

№ 2. В равнобедренной трапеции сумма оснований равна 48 см, а радиус вписанной в нее окружности равен 6√3 см. Найдите стороны трапеции.
ОТВЕТ: 12, 24, 36, 24 см.

Ответы на самостоятельную работу
III уровня сложности

С–15. 3 ур. Вариант 1

№ 1. В прямоугольном треугольнике один из углов равен 30°, радиус вписанной в него окружности равен 5 см. Найдите площадь треугольника.
ОТВЕТ: 75 + 5√3 см2.

№ 2. Расстояния от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны равны 6 и 8 см. Найдите площадь трапеции.
ОТВЕТ: 94,08 см2.

С–15. 3 ур. Вариант 2

№ 1. В прямоугольном треугольнике один из углов равен 60°, радиус описанной в него окружности равен 4 см. Найдите площадь треугольника.
ОТВЕТ: 48 + 32√3 см2.

№ 2. Расстояния от центра вписанной в равнобедренную трапецию окружности до концов боковой стороны равны 9 и 12 см. Найдите площадь трапеции.
ОТВЕТ: 216 см2.

Вы смотрели: Самостоятельная работа № 15 по геометрии в 8 классе с ответами и решениями (3 уровня сложности по 2 варианта). Урок 62. «Свойство описанного четырехугольника» УМК Атанасян и др. (Просвещение). Геометрия 8 класс Самостоятельная 15. Поурочное планирование по геометрии. Выберите дальнейшее действие:

Самостоятельная работа № 16 по геометрии в 8 классе с ответами (2 уровня сложности по 2 варианта, дополнительные задачи). Урок 64. «Свойство вписанного четырехугольника» УМК Атанасян и др. (Просвещение). Геометрия 8 класс Самостоятельная 16. Поурочное планирование по геометрии.

Задача № 1. Докажите, что в любом вписанном четырехугольнике сумма противоположных углов равна 180°.

Задача № 2. Сформулируйте утверждение, обратное свойству вписанного четырехугольника, и выясните его истинность.

Задача № 3. Найдите периметр прямоугольника, вписанного в окружность радиуса 7,5 см, если стороны прямоугольника относятся как 3 : 4.

Задача № 4. В равнобедренном треугольнике АВС с основанием АС проведены высоты AD и СЕ, пересекающиеся в точке Q. Докажите, что около четырехугольника BEQD можно описать окружность.

С–16. 1 ур. Вариант 1

№ 1. Равносторонний треугольник АВС вписан в окружность радиуса 6 см. Найдите его сторону.
ОТВЕТ: 6√3 см.

№ 2. Прямоугольный треугольник с катетами 6 см и 8 см вписан в окружность. Найдите его радиус.
ОТВЕТ: 5 см.

С–16. 1 ур. Вариант 2

№ 1. Равносторонний треугольник MNK со стороной 8 см вписан в окружность. Найдите его радиус.
ОТВЕТ: (8√3)/3 см.

№ 2. Прямоугольный треугольник вписан в окружность радиуса 6,5 см. Найдите площадь треугольника, если один из его катетов равен 5 см.
ОТВЕТ: 30 см2.

С–16. 2 ур. Вариант 1

№ 1. Равнобедренный треугольник с основанием 8 см вписан в окружность радиуса 5 см. Найдите площадь этого треугольника и его боковую сторону.
ОТВЕТ: 32 см2, 4√5 см.

№ 2. Четырехугольник ABCD вписан в окружность с диаметром АС. Найдите утлы четырехугольника, если ∪BC = 100°, ∪CD = 60°.
ОТВЕТ: ∠B = ∠D = 90°, ∠А = 80°, ∠C = 100°.

С–16. 2 ур. Вариант 2

№ 1. Равнобедренный треугольник с высотой, проведенной к основанию и равной 16 см, вписан в окружность радиуса 10 см. Найдите площадь этого треугольника и его боковую сторону.
ОТВЕТ: 128 см2, 8√5 см.

№ 2. Четырехугольник MNKP вписан в окружность с диаметром МК. Найдите утлы четырехугольника, если ∪NK = 140°, ∪РК = 100°.
ОТВЕТ: ∠N = ∠P = 90°, ∠K = 60°, ∠M = 120°.

Ответы на дополнительные задачи

Задача № 2. Сформулируйте утверждение, обратное свойству вписанного четырехугольника, и выясните его истинность.Теорема: Если сумма противолежащих углов четырехугольника равна 180°, то около него можно описать окружность.

ОТВЕТ: 42 см.

Вы смотрели: Самостоятельная работа № 16 по геометрии в 8 классе с ответами и решениями (2 уровня сложности по 2 варианта, доп.задачи). Урок 64. «Свойство вписанного четырехугольника» УМК Атанасян и др. (Просвещение). Геометрия 8 класс Самостоятельная 16. Поурочное планирование по геометрии. Выберите дальнейшее действие:

Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Описанная и вписанная окружности четырёхугольника». Материал для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.

Описанная и вписанная
окружности четырёхугольника

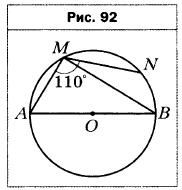
Можно ли описать окружность около четырёхугольника ABCD, если: 1) ∠A = 33°, ∠C = 137°; 2) ∠B = 69°, ∠D = 111° ?
Найдите углы С и D четырёхугольника ABCD, вписанного в окружность, если ∠A = 119°, ∠B = 84°.
Один из углов трапеции, вписанной в окружность, равен 42°. Найдите остальные углы трапеции.
Четырёхугольник ABCD вписан в окружность. Угол А на 58° больше угла В и в 4 раза больше угла С. Найдите углы четырёхугольника.
В четырёхугольнике ABCD известно, что ∠ABC = 68°, ∠ADC = 112°, ∠BAC = 23°, ∠DAC = 52°. Найдите угол между диагоналями четырёхугольника, противолежащий стороне AD.
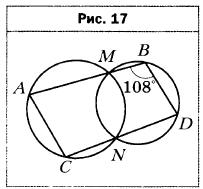
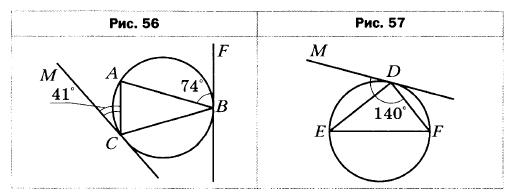
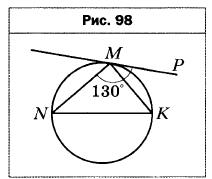
Две окружности пересекаются в точках М и N. Прямая, проходящая через точку М, пересекает окружности в точках А и В, а прямая, проходящая через точку N, — в точках С и D (рис. 17). Найдите угол ВАС, если ∠ABD = 108°.
Равнобокая трапеция вписана в окружность, центр которой лежит на большем основании. Угол между диагоналями трапеции, противолежащий её боковой стороне, равен 32°. Найдите углы трапеции.
В четырёхугольник ABCD вписана окружность. Найдите сторону CD, если АВ = 5 см, ВС = 9 см, AD = 6 см.
Можно ли вписать окружность в четырёхугольник ABCD, если:
1) АВ = 4 см, ВС = 11 см, CD = 12 см, AD = 5 см;
2) АВ = 9 см, ВС = 7 см, CD = 14 см, AD = 15 см?

Основания трапеции, в которую можно вписать окружность, равны 7 см и 9 см. Найдите периметр трапеции.
Средняя линия трапеции равна 14 см, а периметр — 56 см. Докажите, что в данную трапецию можно вписать окружность.
Точка касания окружности, вписанной в равнобокую трапецию, делит её боковую сторону на отрезки, один из которых равен 8 см. Найдите основания трапеции, если её периметр равен 60 см.
Радиус окружности, вписанной в прямоугольную трапецию, равен 6 см, а большая боковая сторона этой трапеции равна 20 см. Найдите среднюю линию трапеции.

Вариант 2

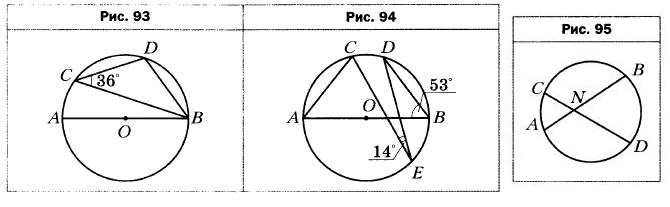
Можно ли описать окружность около четырёхугольника ABCD, если: 1) ∠А = 64°, ∠В = 116°; 2) ∠В = 82°, ∠D = 108°?
Найдите углы А и В четырёхугольника ABCD, вписанного в окружность, если ∠C = 37°, ∠D = 106°.
Один из углов трапеции, вписанной в окружность, равен 114°. Найдите остальные углы трапеции.
Четырёхугольник ABCD вписан в окружность. Угол В на 14° меньше угла С и в 5 раз меньше угла D. Найдите углы четырёхугольника.
В четырёхугольнике ABCD ∠BAD = 74°, ∠BCD = 106°, ∠ABD = 47°, ∠CBD = 58°. Найдите угол между диагоналями четырёхугольника, противолежащий стороне ВС.
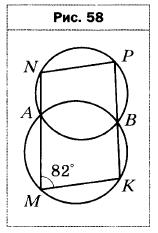
Две окружности пересекаются в точках А и В. Прямая, проходящая через точку А, пересекает окружности в точках М и N, а прямая, проходящая через точку В, — в точках К и Р (рис. 58). Найдите угол MNP, если ∠KMN = 82°.
Равнобокая трапеция вписана в окружность, центр которой лежит на большем основании. Угол между диагоналями трапеции, противолежащий её боковой стороне, равен 44°. Найдите углы трапеции.
В четырёхугольник ABCD вписана окружность. Найдите сторону АВ, если ВС = 4 см, CD = 8 см, AD = 11 см.
Можно ли вписать окружность в четырёхугольник MNPK, если:
1) MN = 4 см, NP = 9 см, PK = 7 см, MK = 3 cm;
2) MN = 9 cm, NP = 5 см, PK = 8 см, MK = 12 cm?
Боковые стороны трапеции, в которую можно вписать окружность, равны 5 см и 11 см. Найдите периметр трапеции.
Средняя линия трапеции равна 16 см, а периметр — 64 см. Докажите, что в данную трапецию можно вписать окружность.
Точка касания окружности, вписанной в равнобокую трапецию, делит её боковую сторону на отрезки, один из которых равен 12 см. Найдите основания трапеции, если её периметр равен 64 см.
Радиус окружности, вписанной в прямоугольную трапецию, равен 8 см, а средняя линия этой трапеции равна 18 см. Найдите большую боковую сторону трапеции.

Вариант 3

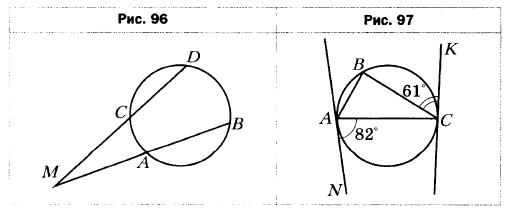
Можно ли описать окружность около четырёхугольника ABCD, если: 1) ∠А = 56°, ∠C = 124°; 2) ∠B = 64°, ∠D = 106°?
Найдите углы А и В четырёхугольника ABCD, вписанного в окружность, если ∠C = 38°, ∠D = 134°.
Один из углов трапеции, вписанной в окружность, равен 56°. Найдите остальные углы трапеции.
Четырёхугольник ABCD вписан в окружность. Угол С на 11° больше угла D и в 8 раз меньше угла А. Найдите углы четырёхугольника.
В четырёхугольнике ABCD известно, что ∠ABC = 124°, ∠ADC = 56°, ∠BАС = 32°, ∠CAD = 54°. Найдите угол между диагоналями четырёхугольника, противолежащий стороне АВ.
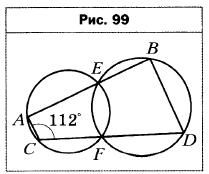
Две окружности пересекаются в точках Е и F. Прямая, проходящая через точку Е, пересекает окружности в точках А и В, а прямая, проходящая через точку F, — в точках С и D (рис. 99). Найдите угол BDC, если ∠ACD = 112°.
Равнобокая трапеция вписана в окружность, центр которой лежит на большем основании. Угол между диагоналями трапеции, противолежащий её боковой стороне, равен 26°. Найдите углы трапеции.
В четырёхугольник ABCD вписана окружность. Найдите сторону ВС, если АВ = 7 см, CD = 10 см, AD =12 см.
Можно ли вписать окружность в четырёхугольник ABCD, если:
1) АВ = 6 см, ВС = 10 см, CD = 11 см, AD = 7 см;
2) АВ = 10 см, ВС = 14 см, CD = 16 см, AD = 11 см?
Боковая сторона равнобокой трапеции, в которую можно вписать окружность, равна 12 см. Найдите периметр трапеции.
Средняя линия трапеции равна 12 см, а периметр — 48 см. Докажите, что в данную трапецию можно вписать окружность.
Точка касания окружности, вписанной в равнобокую трапецию, делит её боковую сторону на отрезки, один из которых равен 5 см. Найдите основания трапеции, если её периметр равен 56 см.
Большая боковая сторона прямоугольной трапеции равна 14 см, а средняя линия этой трапеции равна 10 см. Найдите радиус окружности, вписанной в трапецию.

Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Описанная и вписанная окружности четырёхугольника». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки!

Вернуться к Списку упражнений по геометрии УМК Мерзляк

Геометрия 8 Контрольная 2 (Мерзляк) с ответами. Контрольная работа по геометрии в 8 классе «Средняя линия треугольника. Трапеция. Вписанные и описанные четырёхугольники» для УМК Мерзляк, Полонский, Якир в 4-х вариантов.

Геометрия 8 класс (УМК Мерзляк) Контрольная работа № 2

Тема: Средняя линия треугольника. Трапеция. Вписанные и описанные четырёхугольники

К-2 Вариант 1 (задания)

К-2 Вариант 2 (задания)

Точки F и E – середины сторон BC и BA треугольника ABC соответственно. Найдите периметр треугольника ABC, если BE = 10 см, BF = 16 см, EF = 14 см.
Одно из оснований трапеции в 2 раза больше другого, а её средняя линия равна 6 см. Найдите основания трапеции.
Две противолежащие стороны четырёхугольника равны 10 см и 14 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность?
Меньшее основание равнобокой трапеции равно 4 см, а её боковая сторона – 5 см. Найдите периметр трапеции, если её диагональ делит тупой угол трапеции пополам.
Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠ADB = 62°, ∠ACD = 54°, ∠CBD = 27°.
Диагонали равнобокой трапеции перпендикулярны, её боковая сторона равна 12 см, а периметр – 42 см. Найдите высоту трапеции.

К-2 Вариант 3 (задания)

Точки A и B – середины сторон MN и MK треугольника MNK соответственно. Найдите периметр треугольника AMB, если MN = 14 см, MK = 12 см, NK = 20 см.
Одно из оснований трапеции на 10 см меньше другого, а её средняя линия равна 13 см. Найдите основания трапеции.
Две противолежащие стороны четырёхугольника равны 7 см и 13 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность?
Найдите периметр равнобокой трапеции, если её основания равны 9 см и 14 см, а диагональ делит острый угол трапеции пополам.
Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠ABD = 34°, ∠BDC = 73°, ∠CAD = 24°.
Диагонали равнобокой трапеции перпендикулярны, её высота равна 12 см, а боковая сторона – 15 см. Найдите периметр трапеции.

К-2 Вариант 4 (задания)

Точки C и D – середины сторон FA и FN треугольника FAN соответственно. Найдите периметр треугольника FAN, если FC = 20 см, FD = 22 см, CD = 10 см.
Одно из оснований трапеции в 3 раза меньше другого, а её средняя линия равна 18 см. Найдите основания трапеции.
Две противолежащие стороны четырёхугольника равны 11 см и 19 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность?
Найдите периметр равнобокой трапеции, если её основания равны 12 см и 18 см, а диагональ делит тупой угол трапеции пополам.
Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠ACB = 58°, ∠ABD = 16°, ∠BAC = 44°.
Диагонали равнобокой трапеции перпендикулярны, её периметр равен 50 см, а боковая сторона – 14 см. Найдите высоту трапеции.

На контрольную работу № 2

№ 1. Точки M и K – середины сторон AB и AC треугольника ABC соответственно. Найдите периметр треугольника AMK, если AB = 12 см, BC = 8 см, AC = 14 см. ОТВЕТ: РАМК = 6 + 7 + 4 = 17 см.

№ 2. Одно из оснований трапеции на 6 см больше другого, а её средняя линия равна 9 см. Найдите основания трапеции. ОТВЕТ: 6 см, 12 см.

№ 3. Две противолежащие стороны четырёхугольника равны 9 см и 16 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность? ОТВЕТ: 50 см.

№ 4. Большее основание равнобокой трапеции равно 10 см, а её боковая сторона – 6 см. Найдите периметр трапеции, если её диагональ делит острый угол трапеции пополам. ОТВЕТ: 28 см.

№ 5. Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠ACB = 36°, ∠ABD = 48°, ∠BAC = 85°. ОТВЕТ: ∠B = 59°, ∠D = 121°, ∠A = 96°, ∠C = 84°.

№ 6. Диагонали равнобокой трапеции перпендикулярны, её высота равна 7 см, а периметр – 30 см. Найдите боковую сторону трапеции. ОТВЕТ: 8 см.

ОТВЕТЫ на Вариант 2

№ 1. Точки F и E – середины сторон BC и BA треугольника ABC соответственно. Найдите периметр треугольника ABC, если BE = 10 см, BF = 16 см, EF = 14 см. ОТВЕТ: РАВС = 20 + 32 + 28 = 80 см.

№ 2. Одно из оснований трапеции в 2 раза больше другого, а её средняя линия равна 6 см. Найдите основания трапеции. ОТВЕТ: 4 см, 8 см.

№ 3. Две противолежащие стороны четырёхугольника равны 10 см и 14 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность? ОТВЕТ: 48 см.

№ 4. Меньшее основание равнобокой трапеции равно 4 см, а её боковая сторона – 5 см. Найдите периметр трапеции, если её диагональ делит тупой угол трапеции пополам. ОТВЕТ: 19 см.

№ 5. Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠ADB = 62°, ∠ACD = 54°, ∠CBD = 27°. ОТВЕТ: ∠B = 81°, ∠D = 99°, ∠A = 64°, ∠C = 116°.

№ 6. Диагонали равнобокой трапеции перпендикулярны, её боковая сторона равна 12 см, а периметр – 42 см. Найдите высоту трапеции. ОТВЕТ: 9 см.

ОТВЕТЫ на Вариант 3

№ 1. Точки A и B – середины сторон MN и MK треугольника MNK соответственно. Найдите периметр треугольника AMB, если MN = 14 см, MK = 12 см, NK = 20 см. ОТВЕТ: РАМВ = 7 + 6 + 10 = 23 см.

№ 2. Одно из оснований трапеции на 10 см меньше другого, а её средняя линия равна 13 см. Найдите основания трапеции. ОТВЕТ: 8 см, 18 см.

№ 3. Две противолежащие стороны четырёхугольника равны 7 см и 13 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность? ОТВЕТ: 40 см.

№ 4. Найдите периметр равнобокой трапеции, если её основания равны 9 см и 14 см, а диагональ делит острый угол трапеции пополам. ОТВЕТ: 41 см.

№ 5. Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠ABD = 34°, ∠BDC = 73°, ∠CAD = 24°. ОТВЕТ: ∠B = 58°, ∠D = 122°, ∠A = 97°, ∠C = 83°.

№ 6. Диагонали равнобокой трапеции перпендикулярны, её высота равна 12 см, а боковая сторона – 15 см. Найдите периметр трапеции. ОТВЕТ: 54 см.

ОТВЕТЫ на Вариант 4

№ 1. Точки C и D – середины сторон FA и FN треугольника FAN соответственно. Найдите периметр треугольника FAN, если FC = 20 см, FD = 22 см, CD = 10 см. ОТВЕТ: PFAN = 40 + 44 + 20 = 104 см.

№ 2. Одно из оснований трапеции в 3 раза меньше другого, а её средняя линия равна 18 см. Найдите основания трапеции. ОТВЕТ: 9 см, 27 см.

№ 3. Две противолежащие стороны четырёхугольника равны 11 см и 19 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность? ОТВЕТ: 60 см.

№ 4. Найдите периметр равнобокой трапеции, если её основания равны 12 см и 18 см, а диагональ делит тупой угол трапеции пополам. ОТВЕТ: 66 см.

№ 5. Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠ACB = 58°, ∠ABD = 16°, ∠BAC = 44°. ОТВЕТ: ∠B = 78°, ∠D = 102°, ∠A = 106°, ∠C = 74°.

№ 6. Диагонали равнобокой трапеции перпендикулярны, её периметр равен 50 см, а боковая сторона – 14 см. Найдите высоту трапеции. ОТВЕТ: 11 см.

Вы смотрели: Геометрия 8 Контрольная 2 (Мерзляк). Контрольная работа по геометрии в 8 классе «Средняя линия треугольника. Трапеция. Вписанные и описанные четырёхугольники» для УМК Мерзляк, Полонский, Якир из 4-х вариантов.

Смотреть аналогичную контрольную № 2 с решениями (2 варианта)

Вернуться к Списку контрольных работ из Методички (по 4 варианта)

Цитаты из пособия «Геометрия 8 класс. Методическое пособие / Е. Буцко и др. » использованы в учебных целях.

Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Центральные и вписанные углы». Материал для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.

Центральные и вписанные углы

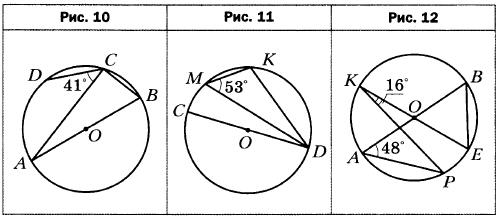
Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Трапеция». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки!