Слайд 9Как запомнить формулу (1) Если в начале записи теоремы мы «встанем» в
вершину A и «пойдем по контуру треугольника» с «заходом» в точки и секущей (назовем их новыми точками), то в каждой дроби будем делить отрезок, соединяющий текущую вершину и новую точку, на отрезок, соединяющий новую точку и следующую вершину (в порядке их обхода по контуру). Или коротко: в числитель заносится отрезок «от вершины до новой точки», а в знаменателе «от новой точки до следующей вершины». И так по кругу. (Движение начинается в точке и в ней же заканчивается).

Теоремы Чевы и Менелая. Учитель математики МБОУ сош28 г.Балаково Покатилова Н.А.
A C1C1 C B1B1 B A1A1 Теорема Чевы: Пусть в треугольнике АВС на сторонах ВС, СА, АВ или на их продолжениях взяты соответственно точки А 1,В 1,С 1, не совпадающие с вершинами треугольника. Прямые АА 1, ВВ 1, и СС 1 пересекаются в одной точке тогда и только тогда, когда:
Теорема Менелая: Пусть в треугольнике АВС на сторонах ВС, СА, АВ или на их продолжениях взяты соответственно точки А 1,В 1,С 1, не совпадающие с вершинами треугольника. Точки А 1, В 1, и С 1 лежат на одной прямой тогда и только тогда, когда: AB1B1 C B A1A1 C1C1
Точка С 1 делит сторону АВ треугольника АВС в отношении 2 : 1. Точка В 1 лежит на продолжении стороны АС за точку С, и АС = СВ 1. В каком отношении делит прямая В 1 С 1 сторону ВС? Задача 1 A B C C1C1 B1B1 A1A1
Задача 2 В треугольнике АВС АD – медиана, точка О – середина медианы. Прямая ВО пересекает сторону АС в точке К. В каком отношении точка К делит АС, считая от точки А?
Задача 3 Пусть АD – медиана треугольника АВС. На стороне АD взята точка К так, что АК : КD = 3 : 1. Прямая ВК разбивает треугольник АВС на два. Найдите отношение площадей этих треугольников.
Задача 4 В треугольнике АВС, описанном около окружности, АВ = 8, ВС = 5, АС = 4. А 1 и С 1 – точки касания, принадлежащие соответственно сторонам ВС и ВА. Р – точка пересечения отрезков АА 1 и СС 1. Точка Р лежит на биссектрисе ВВ 1. Найдите АР : РА 1.
Задача 5 Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.
Задача 6 Биссектрисы ВЕ и АD треугольника АВС пересекаются в точке Q. Найдите площадь треугольника АВС, если площадь треугольника BQD равна 1, 2АС = 3 АВ, 3ВС = 4 АВ.
1. На продолжениях сторон АВ, ВС, АС треугольника АВС взяты соответственно точки С 1, А 1, В 1 так, что АВ = ВС 1, ВС = СА 1, СА = АВ 1. Найдите отношение в котором прямая АВ 1 делит сторону А 1 С 1 треугольника А 1 В 1 С Точки А 1 и В 1 делят стороны ВС и АС треугольника АВС в отношениях 2 : 1 и 1 : 2. Прямые АА 1 и ВВ 1 пересекаются в точке О. Площадь треугольника АВС равна 1. Найдите площадь треугольника ОВС. Домашнее задание
Применение теорем Чевы и Менелая для решения планиметрических задач. Сравнительный анализ в эффективности применения этих теорем по сравнению с другими способами решения планиметрических задач Применение теорем Чевы и Менелая для решения планиметрических задач. Сравнительный анализ в эффективности применения этих теорем по сравнению с другими способами решения планиметрических задач. Выполнил: Димитров Денис, ученик 11 «А» класса. Научный руководитель: Шабунина Е.И., учитель математики МОУ «Лицей 3». МОУ «Лицей 3» г. Саров, 2010 год. г. Саров, 2010 год.
Цель работы – изучить теоремы Чевы и Менелая и рассмотреть применение этих теорем к решению планиметрических задач. Задачей работы стало сравнение и выявление эффективности применения теорем Чевы и Менелая по сравнению с другими способами решения планиметрических задач. Постановка цели, формулировка задачи. 2
Исторические справки. Джованни Чева Менелай Александрийский 3
Теорема Чевы. Если через вершины ABC проведены прямые AX, BY, CZ, пересекающие противоположные стороны (или их продолжения) в точках X, Y, Z, то для того чтобы эти прямые пересекались в одной точке, необходимо и достаточно, чтобы выполнялось условие: 4
Теорема Чевы (первый случай). BAC Z X Y P Рис. 1 5
Теорема Чевы (второй случай). PBX C A Y Z H1H1H1H1 H h1h1h1h1 h Рис. 2 6
Теорема Чевы (доказательство 2). α A Z Y β γ y x m a vB C X P n u z b t c d Рис. 3 Рис. 3 Рис. 4 Рис. 4 ABC XP Y Z α β 7
Теорема Чевы (обратная). ACBX Z T Y P Рис. 5 Рис. 5 8
Теорема Менелая. Если на сторонах ABC или на их продолжениях отмечены точки X, Y, Z так, что X лежит на AB, Y – на BС, Z – на CA, то эти точки будут лежать на одной прямой тогда и только тогда, когда выполнено условие: 9
Теорема Менелая (первый случай). A a b C K ZBY c d e m n X Рис. 6 Рис. 6 10
Теорема Менелая (второй случай). ABC XYZK Рис. 7 Рис. 7 11
Теорема Менелая (доказательство 2). ABC Z X Y l h1h1h1h1 h2h2h2h2 h3h3h3h3 n m d c a b Рис. 8 Рис. 8 l X YZ ABC h1h1h1h1 h2h2h2h2 h3h3h3h3 Рис. 9 Рис. 9 12
Теорема Менелая (обратная). X ABCZ T Y Рис. 10 Рис
Задача 1. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины. 14
Задача 1. I способ (без использования теорем Чевы и Менелая). ACB B1B1B1B1 A1A1A1A1 C1C1C1C1 O (O 1 ) Рис
Задача 1. II способ (c использованием теорем Чевы и Менелая). ACB B1B1B1B1 A1A1A1A1 C1C1C1C1 O Рис
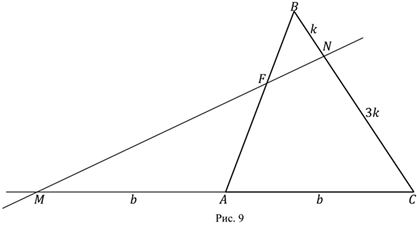
Задача 2. В ABC на стороне BC взята точка N так, что NC=3BN. На продолжении стороны AC за точку A взята точка M так, что MA=AC. Прямая MN пересекает сторону AB в точке F. Найти отношение BF:FA. 17
Задача 2. I способ (без использования теоремы Менелая). AMC NBF K bb k 3k Рис
Задача 2. II способ (c использованием теоремы Менелая). AMC NBF bb k 3k Рис. 14 Рис
Задача 3. Пусть AD – медиана ABC. На медиане AD взята точка K так, что AK:KD=3:1. Прямая BK разбивает ABC на два треугольника: ABP и CBP, причём BKAC=P. Найти отношение S ABP :S CBP. 20
Задача 3. I способ (без использования теоремы Менелая). APC DM K B m 3m a a Рис. 15 Рис
Задача 3. II способ (c использованием теоремы Менелая). APC D K B m 3m a a Рис. 16 Рис
Теоремы Чевы и Менелая не изучаются в основном курсе геометрии 7 –9 классов. Но трудности, связанные с освоением этих теорем, оправданы их применением при решении задач. Теоремы Чевы и Менелая не изучаются в основном курсе геометрии 7 –9 классов. Но трудности, связанные с освоением этих теорем, оправданы их применением при решении задач. Решение задач с помощью теорем Чевы и Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными. Решение задач с помощью теорем Чевы и Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными. Я считаю, что теоремы Чевы и Менелая должны быть включены в основной курс геометрии 7 –9 классов, так как решение задач с помощью этих теорем развивает мышление и логику учеников. Я считаю, что теоремы Чевы и Менелая должны быть включены в основной курс геометрии 7 –9 классов, так как решение задач с помощью этих теорем развивает мышление и логику учеников. Заключение. 23

Теорема Менелая и ее применение при решении задач (подготовка к ЕГЭ) Методическая разработка Рудаковой Татьяны Викторовны Учителя математики МБОУ «Гимназия № 2» г. Курчатова Курской области

Содержание 1. а) б) 2. 3. Теоретические факты: пропорциональные отрезки в треугольниках отношение площадей треугольников. Теорема Менелая. Применение теоремы для решения задач.
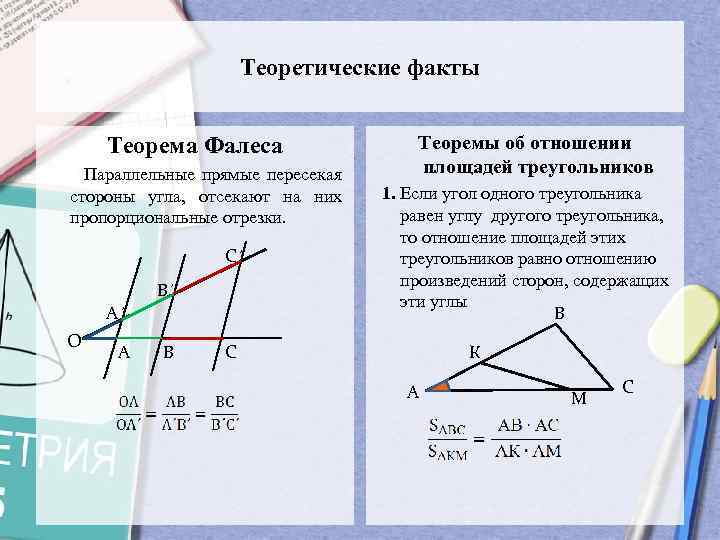
Теоретические факты Теорема Фалеса Параллельные прямые пересекая стороны угла, отсекают на них пропорциональные отрезки. С´ В´ А´ О А В Теоремы об отношении площадей треугольников 1. Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, содержащих эти углы В С К А М С
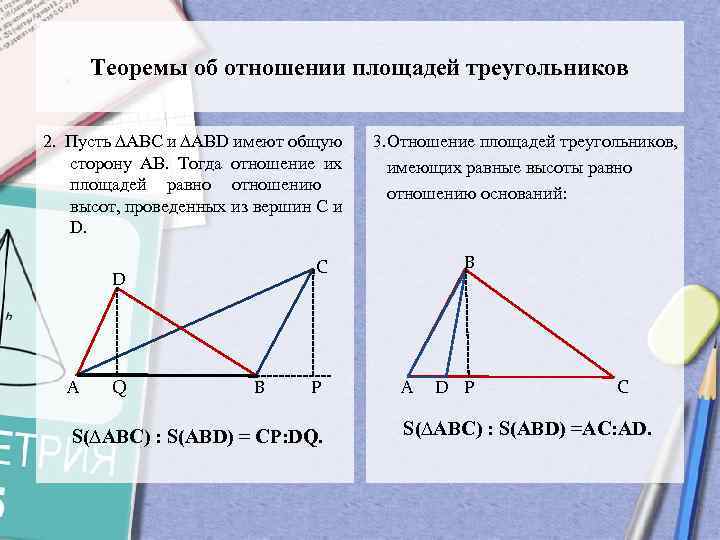
Теоремы об отношении площадей треугольников 2. Пусть ∆АВС и ∆АВD имеют общую сторону АВ. Тогда отношение их площадей равно отношению высот, проведенных из вершин С и D. Q В С D А 3. Отношение площадей треугольников, имеющих равные высоты равно отношению оснований: В P S(∆АВС) : S(АВD) = СР: DQ. А D P С S(∆АВС) : S(АВD) =AC: АD.
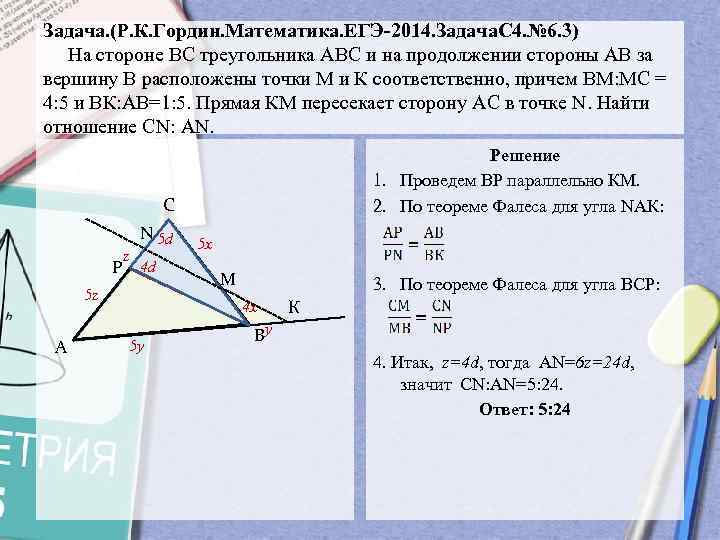
Задача. (Р. К. Гордин. Математика. ЕГЭ-2014. Задача. С 4. № 6. 3) На стороне ВС треугольника АВС и на продолжении стороны АВ за вершину В расположены точки М и К соответственно, причем ВМ: МС = 4: 5 и ВК: АВ=1: 5. Прямая КМ пересекает сторону АС в точке N. Найти отношение СN: АN. Решение 1. Проведем ВР параллельно КМ. 2. По теореме Фалеса для угла NАК: С z N 5 d N Р 4 d 5 z А 5 х М 4 х 4 x 5 у 3. По теореме Фалеса для угла ВСР: К Ву 4. Итак, z=4 d, тогда АN=6 z=24 d, значит СN: АN=5: 24. Ответ: 5: 24

Предложенный вариант решения задачи – один из традиционных, без применения теоремы Менелая. Рассмотрим другой (более рациональный) способ решения, применяя указанную теорему Теорема Менелая Пусть на сторонах AB, BC и на продолжении стороны AC ∆ABC взяты соответственно точки С´, А´ и В´, не совпадающие с вершинами ∆ABC. Точки лежат на одной прямой тогда и только тогда, когда выполняется равенство Для дальнейшего решения задач воспользуемся необходимым условием данной теоремы.
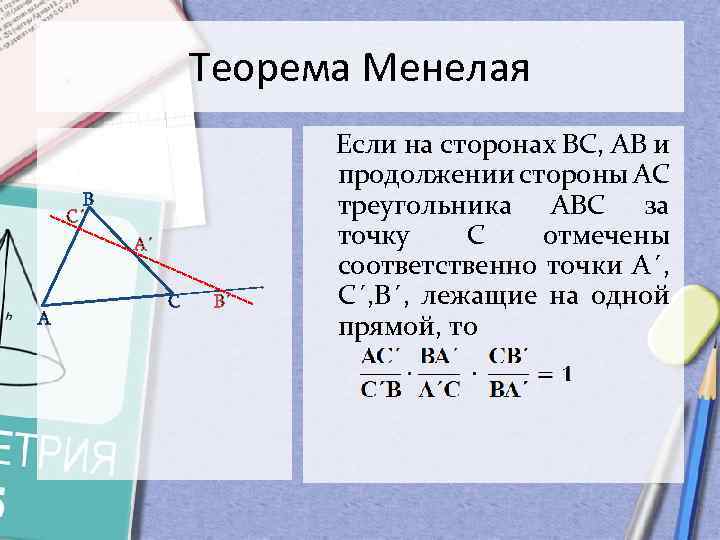
Теорема Менелая В С´ А´ А С В´ Если на сторонах ВС, АВ и продолжении стороны АС треугольника АВС за точку С отмечены соответственно точки А´, С´, В´, лежащие на одной прямой, то
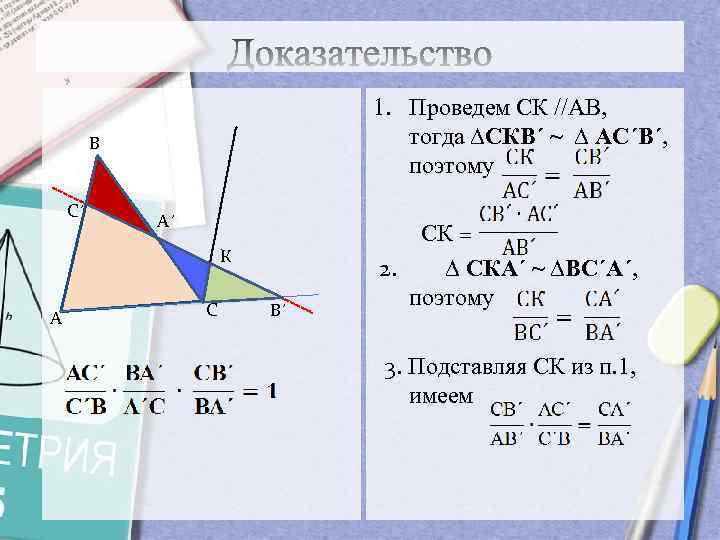
1. Проведем СК //АВ, тогда ∆СКВ´ ~ ∆ АС´В´, поэтому В С´ А´ К А С В´ СК = 2. ∆ СКА´ ~ ∆ВС´А´, поэтому 3. Подставляя СК из п. 1, имеем
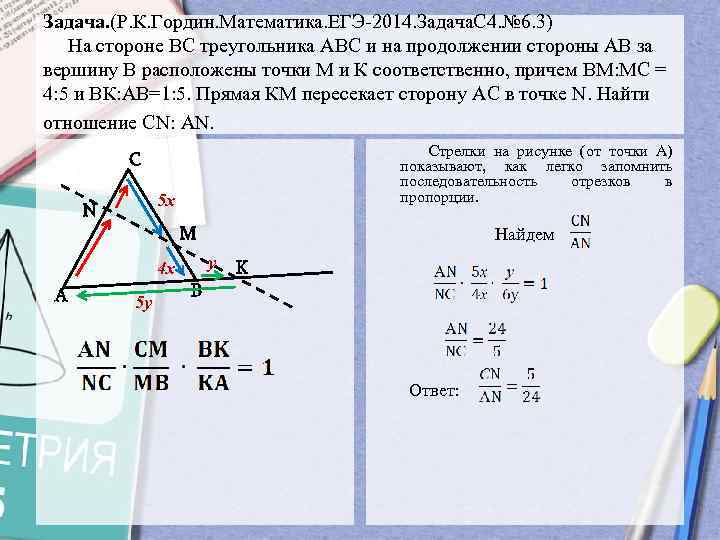
Задача. (Р. К. Гордин. Математика. ЕГЭ-2014. Задача. С 4. № 6. 3) На стороне ВС треугольника АВС и на продолжении стороны АВ за вершину В расположены точки М и К соответственно, причем ВМ: МС = 4: 5 и ВК: АВ=1: 5. Прямая КМ пересекает сторону АС в точке N. Найти отношение СN: АN. Стрелки на рисунке (от точки А) показывают, как легко запомнить последовательность отрезков в пропорции. С 5 х N M у 4 х А 5 у Найдем K В Ответ:
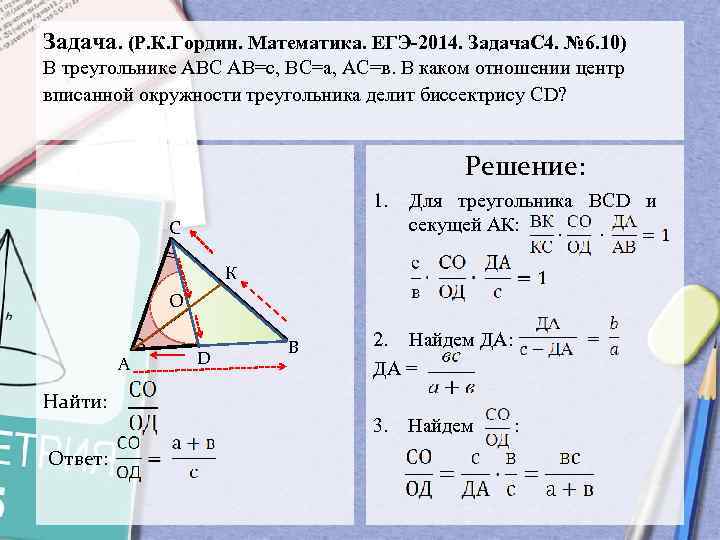
Задача. (Р. К. Гордин. Математика. ЕГЭ-2014. Задача. С 4. № 6. 10) В треугольнике АВС АВ=с, ВС=а, АС=в. В каком отношении центр вписанной окружности треугольника делит биссектрису СD? Решение: 1. С Для треугольника ВСD и секущей АК: К О А D В 2. Найдем ДА: ДА = = Найти: 3. Ответ: Найдем :

Задача. (Р. К. Гордин. Математика. ЕГЭ-2014. Задача С 4. № 6. 14) В ∆АВС, площадь которого равна 6, на стороне АВ взята т. К, делящая эту сторону в отношении АК: ВК=2: 3, а на стороне АС взята т. L, делящая АС в отношении. AL: LС=5: 3. Точка Q пересечения прямых СК и ВL отстоит от прямой АВ на расстояние 1, 5. Найти сторону АВ. Решение: 1. Для тр. АСК и секущей ВL найдем отношение CQ: QK. С 3 y L Q 5 y А Р 2 x H К 3 x В 2. Проведем высоту СР. СР// QH. 3. По теореме Фалеса Н – середина РК, тогда QH-средняя линия СРК, значит СР=3. 4. S (АВС) =0, 5 АВ • СР, тогда АВ=2 S(АВС) : СР=4. Ответ: АВ = 4.

Задача. ( Математика ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под редакцией А. Л. Семенова, И. В. Ященко. Трениров. работа 28. С 4) На сторонах АВ, ВС и АС ∆АВС взяты соответственно точки К, L и М, причем АК: КВ=2: 3, ВL: LС=1: 2, СМ: МА=3: 1. В каком отношении отрезок КL делит отрезок ВМ? Решение: В у 3 х 2 х Р 2 z А Найти Ответ: 1. Для ∆АВС и секущей КL: L О К z М 2 у 3 z 2. АР = С РС = АС = 4 z =2 z, значит = 3. Для ∆АВМ и секущей КL:

Задача. (Сайт А. А. Ларина. Тренировочный вариант № 67. от 09. 03. 2014. С 4) В ∆АВС на сторонах АВ, ВС, и СА отложены соответственно отрезки АD =⅓ АВ, ВЕ = ⅓ ВС, СF = ⅓ CА. а) доказать, что , где М = АЕ ∩ СD, К = СD ∩ ВF, N = АЕ∩ВF. б) найти, какую часть от площади ∆АВС составляет площадь ∆MNK. 1. Для ∆АВF и секущей DC: а) докажем, что В у Е 2 х D х А N М 2 у 2. Для ∆АЕС и секущей FВ: К 2 z F z С 3. Для ∆DBC и секущей ЕА аналогично
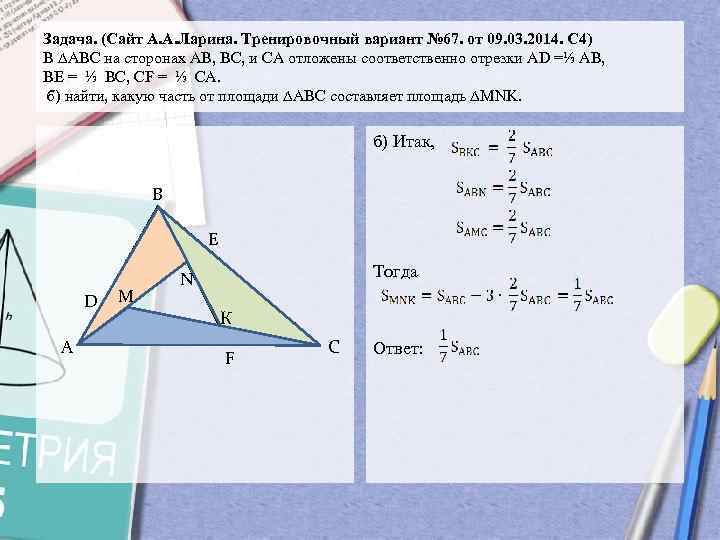
Задача. (Сайт А. А. Ларина. Тренировочный вариант № 67. от 09. 03. 2014. С 4) В ∆АВС на сторонах АВ, ВС, и СА отложены соответственно отрезки АD =⅓ АВ, ВЕ = ⅓ ВС, СF = ⅓ CА. б) найти, какую часть от площади ∆АВС составляет площадь ∆MNK. б) Итак, В E D А М М Тогда N К K F С Ответ:

Заключение Решение задач с помощью теоремы Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными. Теорема Менелая помогает быстро и оригинально решить задачи повышенной сложности, в том числе и задачи уровня С единого государственного экзамена. Используемая литература § § § ЕГЭ 2014. Математика. Задача С 4. Гордин Р. К. Под ред. Семенова А. Л. 2013 г. Математика. ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под ред. А. Л. Семенова, И. В. Ященко. 2014 г. http: //alexlarin. net/ege/2014/trvar 67. html

Теорема Менелая и ее применение при решении задач (подготовка к ЕГЭ)
Рудаковой Татьяны Викторовны
Учителя математики МБОУ «Гимназия № 2»
г. Курчатова Курской области

- Теоретические факты:
а) пропорциональные отрезки в треугольниках
б) отношение площадей треугольников.
- Теорема Менелая.
- Применение теоремы для решения задач.
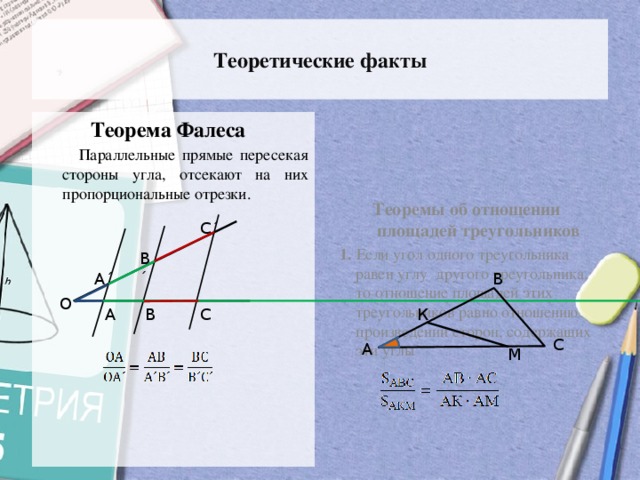
Теоремы об отношении площадей треугольников
1. Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, содержащих эти углы
Параллельные прямые пересекая стороны угла, отсекают на них пропорциональные отрезки.
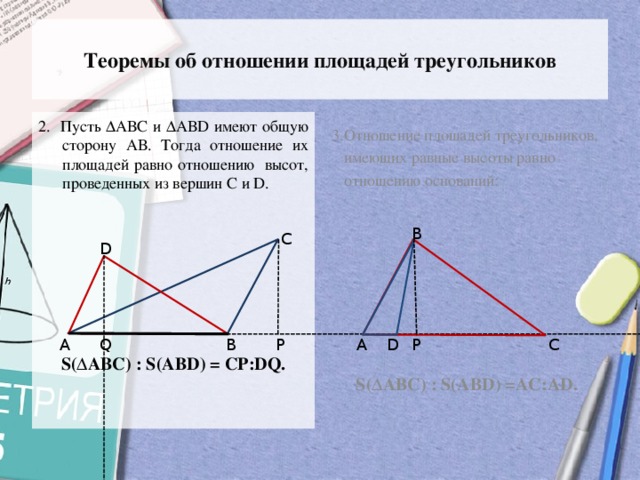
Теоремы об отношении площадей треугольников
3.Отношение площадей треугольников,
2. Пусть ∆АВС и ∆АВD имеют общую сторону АВ. Тогда отношение их площадей равно отношению высот, проведенных из вершин С и D.
имеющих равные высоты равно
S(∆АВС) : S(АВD) = СР:DQ.
S(∆АВС) : S(АВD) =AC:АD.
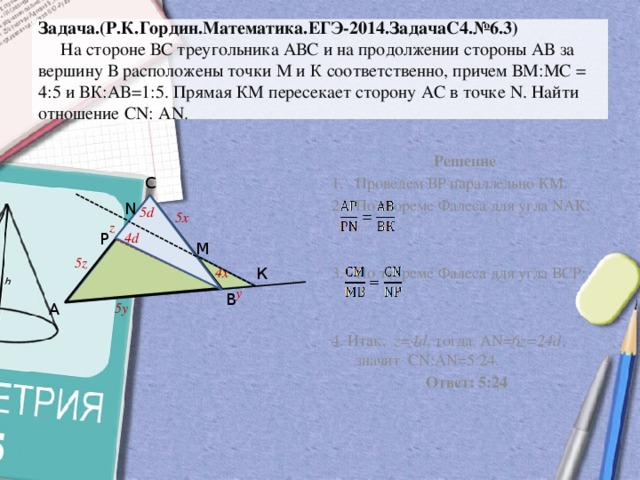
Задача.(Р.К.Гордин.Математика.ЕГЭ-2014.ЗадачаС4.№6.3) На стороне ВС треугольника АВС и на продолжении стороны АВ за вершину В расположены точки М и К соответственно, причем ВМ:МС = 4:5 и ВК:АВ=1:5. Прямая КМ пересекает сторону АС в точке N. Найти отношение СN: АN.
- Проведем ВР параллельно КМ.
- По теореме Фалеса для угла NАК:
- По теореме Фалеса для угла ВСР:
4. Итак, z=4d , тогда АN= 6z=24d , значит СN:АN=5:24.

Предложенный вариант решения задачи – один из традиционных, без применения теоремы Менелая.
Рассмотрим другой (более рациональный) способ решения, применяя указанную теорему
Пусть на сторонах AB, BC и на продолжении стороны AC ∆ABC взяты соответственно точки С´, А´ и В´, не совпадающие с вершинами ∆ABC. Точки лежат на одной прямой тогда и только тогда, когда выполняется равенство
Для дальнейшего решения задач воспользуемся необходимым условием данной теоремы.

Если на сторонах ВС, АВ и продолжении стороны АС треугольника АВС за точку С отмечены соответственно точки А´, С´,В´, лежащие на одной прямой, то
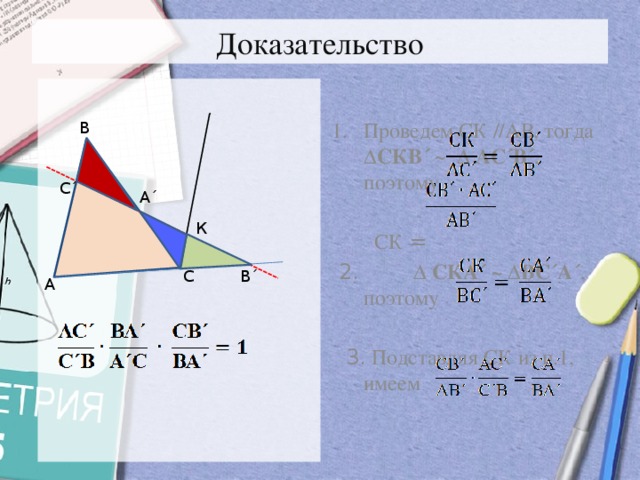
- Проведем СК //АВ, тогда ∆СКВ´ ~ ∆ АС´В´ , поэтому
2. ∆ СКА´ ~ ∆ВС´А´ , поэтому
3. Подставляя СК из п.1, имеем
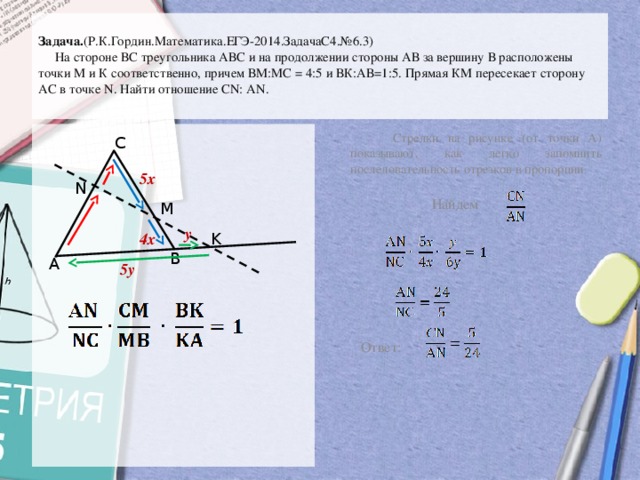
Задача. (Р.К.Гордин.Математика.ЕГЭ-2014.ЗадачаС4.№6.3) На стороне ВС треугольника АВС и на продолжении стороны АВ за вершину В расположены точки М и К соответственно, причем ВМ:МС = 4:5 и ВК:АВ=1:5. Прямая КМ пересекает сторону АС в точке N. Найти отношение СN: АN.
Стрелки на рисунке (от точки А) показывают, как легко запомнить последовательность отрезков в пропорции .
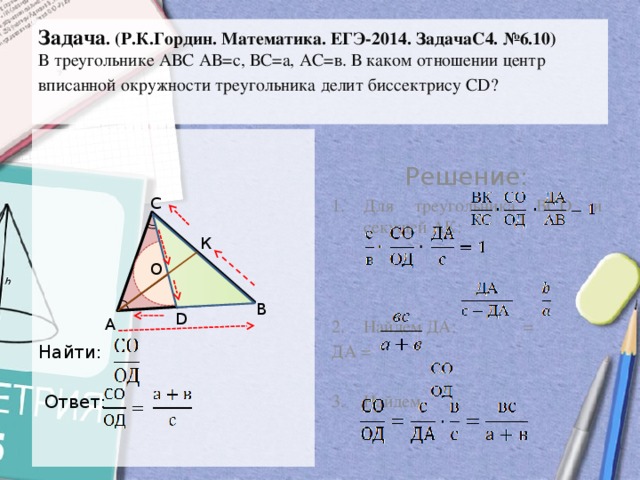
Задача . (Р.К.Гордин. Математика. ЕГЭ-2014. ЗадачаС4. №6.10) В треугольнике АВС АВ=с, ВС=а, АС=в. В каком отношении центр вписанной окружности треугольника делит биссектрису СD?
- Для треугольника ВСD и секущей АК:
- Найдем ДА: =
3. Найдем :
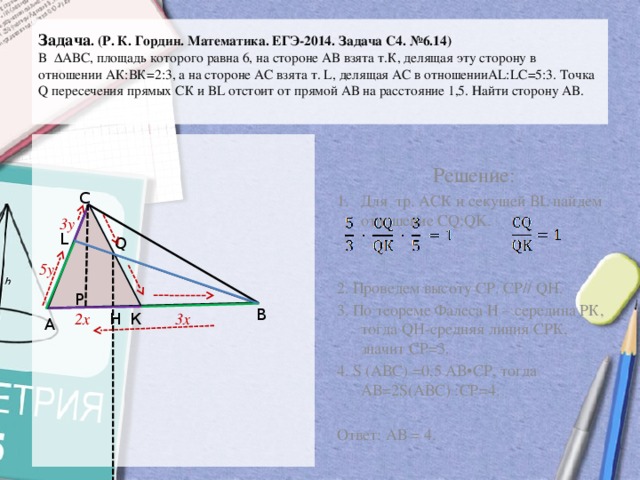
Задача . (Р. К. Гордин. Математика. ЕГЭ-2014. Задача С4. №6.14) В ∆ АВС, площадь которого равна 6, на стороне АВ взята т.К, делящая эту сторону в отношении АК:ВК=2:3, а на стороне АС взята т. L, делящая АС в отношенииAL:LС=5:3. Точка Q пересечения прямых СК и ВL отстоит от прямой АВ на расстояние 1,5. Найти сторону АВ.
- Для тр. АСК и секущей ВL найдем отношение CQ:QK.
2. Проведем высоту СР. СР// QH.
3. По теореме Фалеса Н – середина РК, тогда QH-средняя линия СРК, значит СР=3.
4. S (АВС) =0,5 АВ•СР, тогда АВ=2S(АВС) :СР=4.
Ответ: АВ = 4.
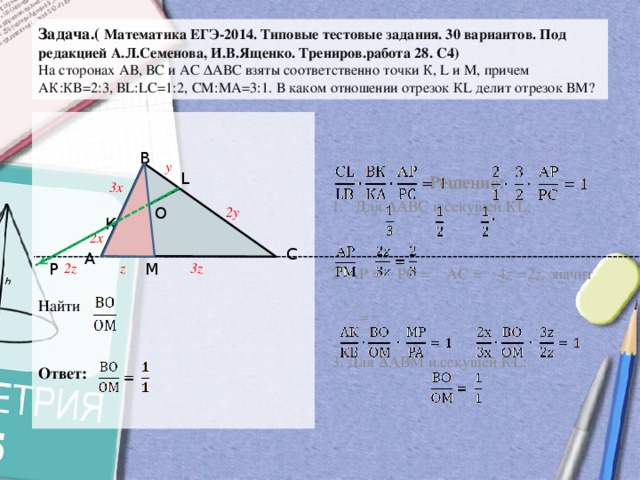
Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под редакцией А.Л.Семенова, И.В.Ященко. Трениров.работа 28. С4) На сторонах АВ, ВС и АС ∆АВС взяты соответственно точки К, L и М, причем АК:КВ=2:3, ВL:LС=1:2, СМ:МА=3:1. В каком отношении отрезок КL делит отрезок ВМ?
- Для ∆АВС и секущей КL:
2. АР = РС = АС = 4 z = 2 z, значит
3. Для ∆АВМ и секущей КL:

Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от 09.03.2014. С4) В ∆АВС на сторонах АВ, ВС, и СА отложены соответственно отрезки АD =⅓ АВ, ВЕ = ⅓ ВС, СF = ⅓ CА. а) доказать, что , где М = АЕ ∩ СD, К = СD ∩ ВF, N = АЕ∩ВF. б) найти, какую часть от площади ∆АВС составляет площадь ∆MNK.
- Для ∆АВF и секущей DC:
а) докажем, что
2. Для ∆АЕС и секущей FВ:
3. Для ∆DBC и секущей ЕА аналогично
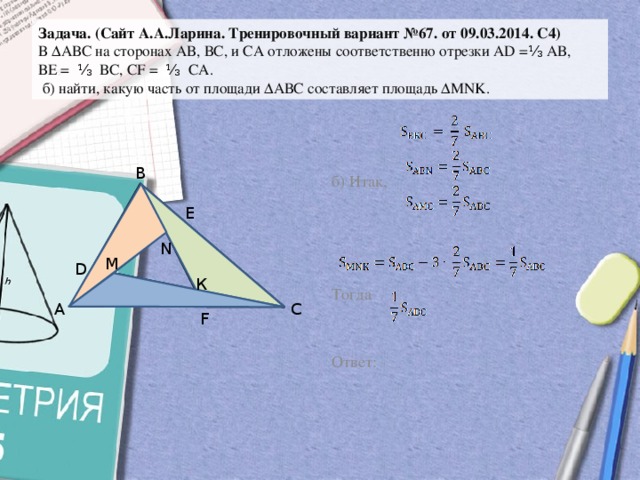
Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от 09.03.2014. С4) В ∆АВС на сторонах АВ, ВС, и СА отложены соответственно отрезки АD =⅓ АВ, ВЕ = ⅓ ВС, СF = ⅓ CА. б) найти, какую часть от площади ∆АВС составляет площадь ∆MNK.

Заключение Решение задач с помощью теоремы Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными. Теорема Менелая помогает быстро и оригинально решить задачи повышенной сложности, в том числе и задачи уровня С единого государственного экзамена.
- ЕГЭ 2014.Математика. Задача С4. Гордин Р.К. Под ред. Семенова А.Л.2013г.
- Математика. ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под ред. А.Л.Семенова, И.В.Ященко. 2014г.
- http://alexlarin.net/ege/2014/trvar67.html
Запольских М.В.
МБОУ Школа №156, г. Уфа, р. Башкортастан
Шамиева Инга Энгелевна (г. Уфа, МБОУ Школы №156)
1. Атанасян, Л.С. Доп. главы к шк. учеб. 8 кл.: Учеб. Пособие для учащихся шк. и классов с углубл. изуч. математики / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.:Просвещение, 1996. – 205с.
2. Вольфсон, , Б. Подготовка к ЕГЭ и ГИА-9: учимся решать задачи / Б. И. Вольфсон, Л. И. Резницкий – Легион, 2011 г. – 129c.
3. Шевкин А. Вокруг теорем Чевы и Менелая //Математика. — № 9. — 2011.
5. Школа в «Кванте», 1996 год, Математика, №6
Нередко учащиеся 9 и 11 классов сталкиваются с трудностями при решении практических задач на экзамене по математике. Это вторая часть ОГЭ/ЕГЭ, которая является наиболее сложной, и, соответственно, за которую можно набрать хорошее число баллов. Знание теорем Чевы и Менелая может значительно упростить решение таких задач.
Помимо экзаменов, изучение данной темы может помочь на олимпиадах, вступительных испытаниях и просто для погружения в удивительный математический мир.
Объект исследования: геометрические задачи, требующие нахождения отношений длин отрезков, площадей фигур.
Гипотеза: применение теорем Чевы и Менелая при решении многих задач рациональнее, чем другие способы решения.
Цель работы: Доказать теоремы Чевы и Менелая, выяснить, насколько их применение упрощает решение задач на отношение отрезков и площадей фигур.
· Рассмотреть доказательство теорем Чевы и Менелая
· Решить несколько задач с их помощью и другими способами. Выяснить какой из методов рациональнее в каждом конкретном случае
· Создать банк задач, при решении которых применение теорем Чевы и Менелая предпочтительнее.
Результатом исследования является презентация, которая поможет выпускникам 9 и 11 классов познакомится с методом решения задач на нахождение отношений длин отрезков и площадей фигур с помощью теорем Чевы и Менелая.
2.1 Теорема Чевы
2.1.1 Кто такой Чева? Джованни Чева (1648-1734 г.)- итальянский инженер и математик. Основной заслугой Чевы является построение учения о секущих, которое положило начало новой – синтетической геометрии; оно изложено в сочинении «О взаимнопересекающихся прямых»(1678).

2.1.2 Что такое чевиана? Определение. Чевианой треугольника называется отрезок, соединяющий вершину треугольника с произвольной точкой противолежащей стороны, или ее продолжения.
1.1.3 Теорема Чевы
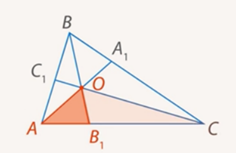
Если на сторонах AB, BC и AC треугольника ABC взяты соответственно точки C1, A1 и B1, то отрезки AA1, BB1 и CC1 пересекаются в одной точке тогда и только тогда, когда: 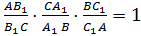
Рассмотрим треугольники AOB1 и COB1
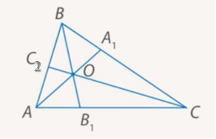
Поскольку их основания лежат на одной прямой, то у этих треугольников общая высота, опущенная из точки O. Отсюда следует, что площади этих треугольников относятся так же, как их основания: 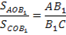
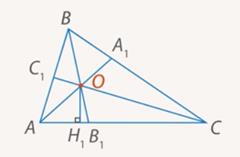
Аналогично можно выписать еще два соотношения:
Перемножая эти три равенства получаем:
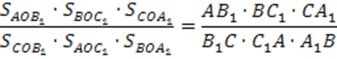
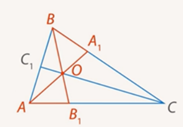
Рассмотрим левую часть данного равенства. Запишем её иначе.
Треугольники AOB1 и BOA1 имеют равные углы. Значит, их площади относятся как произведения длин сторон, заключающих эти углы.
Аналогично можно выписать еще два соотношения:
Перемножив эти равенства, получаем:
Докажем обратное утверждение.
 Пусть точки C1, A1, B1 взяты на сторонах так, что выполнено равенство:
Пусть точки C1, A1, B1 взяты на сторонах так, что выполнено равенство:
Докажем, что отрезки AA1, BB1, CC1 пересекаются в одной точке.
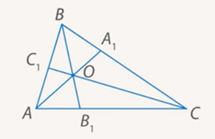
Обозначим буквой O точку пересечения отрезков AA1 и BB1 и проведем прямую CO. Она пересекает сторону AB в некоторой точке, которую обозначим C2. Т.к. отрезки AA1, BB1 и CC2 пересекаются в одной точке, то, по доказанному в первом пункте: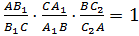 (2)
(2)
Сопоставляя равенства (1) и (2): 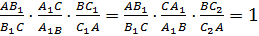 ,
,
приходим к равенству 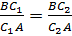 ; которое показывает, что точки C1 и C2 делят сторону AB в одном и том же отношении. Следовательно, точки
; которое показывает, что точки C1 и C2 делят сторону AB в одном и том же отношении. Следовательно, точки
C1 и C2 совпадают, и, значит, отрезки AA1, BB1 и CC1 пересекаются в точке O.
1.2 Теорема Менелая

1.2.1 Кто такой Менелай? Древнегреческий математик и астроном. Автор работ по сферической тригонометрии: 6 книг о вычислении хорд и 3 книги “Сферики” (сохранились в арабском переводе). Для получения формул сферической тригонометрии использовал теорему о прямой, пересекающей стороны треугольника (теорема Менелая).
1.2.2 Формулировка и доказательство теоремы Менелая
Дан треугольник ABC. На прямых AB, BC и AC отмечены точки C1, A1 и B1 соответственно. Точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда:
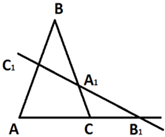
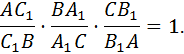
1. Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B1C1.
Треугольники AC1B1 и CKB1 подобны по двум углам.
Следовательно, 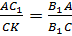 .
. 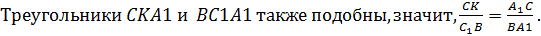
Далее, перемножив полученные равенства, получим:
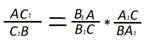 ,откуда следует, что:
,откуда следует, что: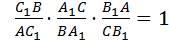
2. Докажем обратное утверждение. Пусть точка B1 взята на продолжении стороны AC, а точки C1 и A1 – на сторонах AB и BC, причем так, что выполнено равенство: 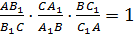
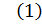
Докажем, что точки A1, B1, C1 лежат на одной прямой. (рис.2)
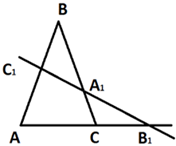
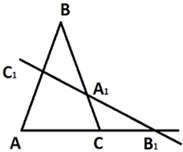
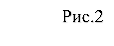



Прямая B1C1 пересекает сторону BC в некоторой точке A2. (рис.1)
Т.к. точки B1, C1, A2 лежат на одной прямой, то по доказанному в первом пункте: 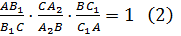
Сопоставляя (1) и (2), приходим к равенству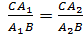 , которое показывает, что точки A1 и A2 делят сторону BC в одном и том же отношении. Следовательно, точки A1 и A2 совпадают, и, значит, точки A1, B1, C1 лежат на одной прямой.
, которое показывает, что точки A1 и A2 делят сторону BC в одном и том же отношении. Следовательно, точки A1 и A2 совпадают, и, значит, точки A1, B1, C1 лежат на одной прямой. 
С помощью теорем Чевы и Менелая нетрудно доказать теоремы о четырех замечательных точках треугольника, теоремы Ван-Обеля и Симпсона. Остановимся на двух последних теоремах подробнее.
3.1 Теорема Ван-Обеля
Пусть чевианы AA1, BB1, CC1 треугольника ABC пересекаются в точке T, тогда справедливо равенство:
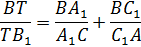
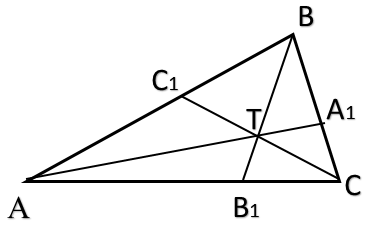
1.Для треугольника ABB1 и секущей CC1 запишем теорему Менелая:
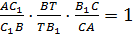 ; откуда получим
; откуда получим 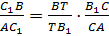 (1)
(1)
2. Для треугольника BB1С и секущей A1A, запишем теорему Менелая:
и секущей A1A, запишем теорему Менелая:
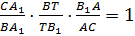 ; откуда следует, что:
; откуда следует, что: 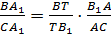 (2)
(2)
3. Сложив 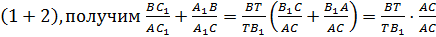 =
= 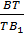 .
.
Итак, 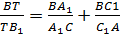 .
.
Теорема Симсона (Симпсона)
Пусть D – произвольная точка описанной около треугольника ABC окружности. DP, DR, DQ – перпендикуляры к сторонам AB, AC и продолжению стороны BC соответственно. Докажем, что основания перпендикуляров P, R, Q лежат на одной прямой
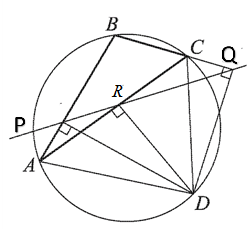
Основания перпендикуляров, проведенных к сторонам треугольника (или их продолжениям) из произвольный точки описанной окружности, лежат на одной прямой
Доказательство (Способ 1.)
Сделаем доп. построение – проведем отрезки AD и CD.
1) Т.к. ∠APD = 90° и ∠ ARD=90°,
то точки A,P,R,D лежат на одной окружности с диаметром AD.
Тогда ∠PRA = ∠PDA, т.к. они опираются на одну дугу.
2) Т.к. ∠CQD= ∠CRD=90°,
то точки Q, C, R, D лежат на одной окружности с диаметром CD.
Следовательно вписанные углы ∠CRQ = ∠CDQ как опирающиеся на одну дугу.
∠PDA = 90° – ∠PAD = 90° – ∠BAD
∠QDC = 90° – ∠QCD = 90° – (180° – ∠BCD) = 90° – ∠BAD
Итак, ∠PDA = ∠QDC, следовательно, ∠PRA = ∠CRQ.
Это означает, что точки P, R, Q лежат на одной прямой.

3.3 Решение задач с помощью теорем Чевы, Менелая, Ван-Обеля и Симпсона
3.3.1 Задача №1
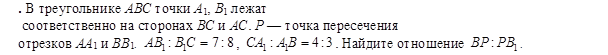
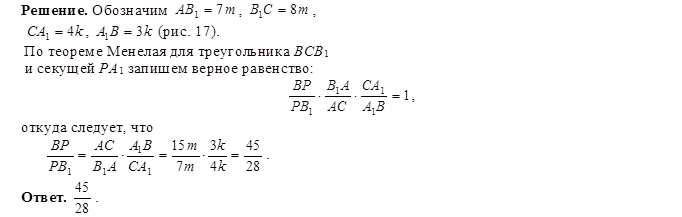
3.3.2 Задача №2
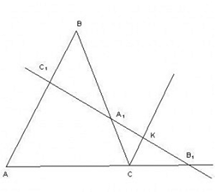
Дано: Три окружности с центрами А, В, С, радиусы которых относятся как 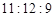 , касаются друг друга внешним образом в точках X, Y, Z как показано на рисунке 19. Отрезки AX и BY пересекаются в точке O. В каком отношении, считая от точки B, отрезок CZ делит отрезок BY?
, касаются друг друга внешним образом в точках X, Y, Z как показано на рисунке 19. Отрезки AX и BY пересекаются в точке O. В каком отношении, считая от точки B, отрезок CZ делит отрезок BY?
Решение. Обозначим 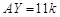 ,
, 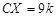 ,
, 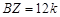 (рис. 19). Так как
(рис. 19). Так как 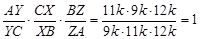 , то по утверждению б) теоремы Чевы отрезки АX, BY и СZ пересекаются в одной точке — точке O. Тогда отрезок CZ делит отрезок BY в отношении
, то по утверждению б) теоремы Чевы отрезки АX, BY и СZ пересекаются в одной точке — точке O. Тогда отрезок CZ делит отрезок BY в отношении 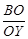 . Найдем это отношение.
. Найдем это отношение.
По теореме Менелая для треугольника BCY и секущей OX имеем: 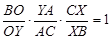 , откуда следует, что
, откуда следует, что 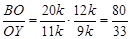 .
.
3.3.4 Задача №4
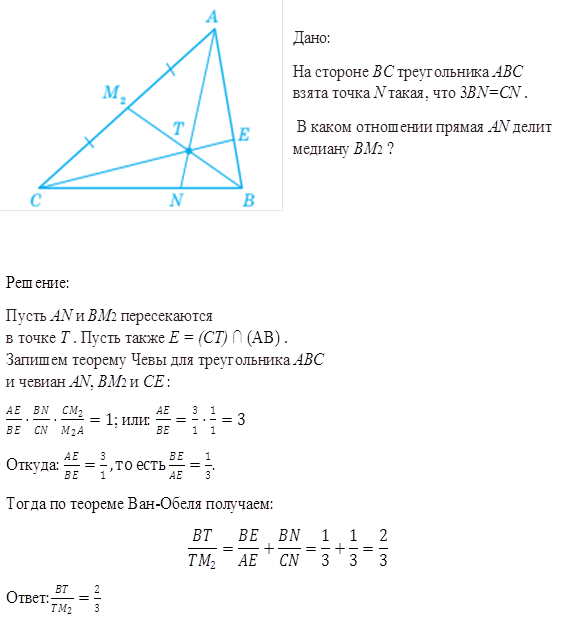

3.3.6. Задача №6
В 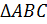 на стороне
на стороне 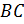 взята точка
взята точка 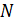 так, что
так, что 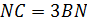 . На продолжении стороны
. На продолжении стороны 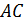 за точку
за точку 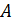 взята точка
взята точка 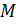 так, что
так, что 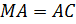 . Прямая
. Прямая 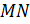 пересекает сторону
пересекает сторону 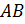 в точке
в точке 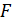 . Найти отношение
. Найти отношение 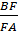 .
.
Дано: 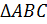 ,
, 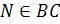 ,
, 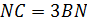 ,
, 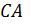 – луч,
– луч, 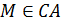 ,
, 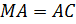 ,
, 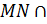
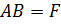 .
.
Найти отношение 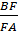 .
.
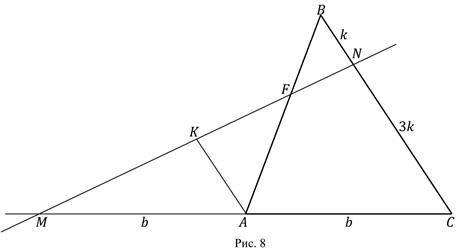
Решение. I способ (без использования теоремы Менелая).
Сделаем дополнительное построение: проведём отрезок 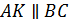 (рис.8) . Пусть
(рис.8) . Пусть 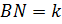 , тогда
, тогда 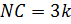 ; пусть
; пусть 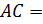
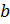 , тогда
, тогда 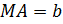 .
.
1) Рассмотрим 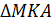 и
и 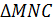 .
.
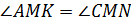 – общий угол для
– общий угол для 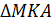 и
и 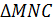 ;
;
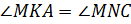 как соответственные углы, образованные при пересечении параллельных прямых
как соответственные углы, образованные при пересечении параллельных прямых 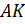 и
и 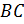 (
(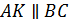 по дополнительному построению) секущей
по дополнительному построению) секущей 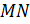 ,
, 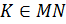 . Следовательно,
. Следовательно, 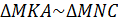 по двум углам.
по двум углам.
Итак, 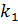 – коэффициент подобия:
– коэффициент подобия: 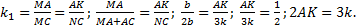
2) Рассмотрим 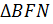 и
и 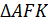 .
.
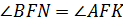 как вертикальные углы;
как вертикальные углы;
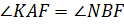 как накрест лежащие углы, образованные при пересечении параллельных прямых
как накрест лежащие углы, образованные при пересечении параллельных прямых 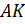 и
и 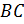 секущей
секущей 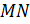 ,
, 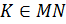 ,
, 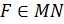 .
.
Следовательно, 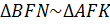 по двум углам.
по двум углам.
Итак, 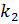 – коэффициент подобия:
– коэффициент подобия: 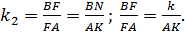
Но, так как по доказанному: 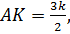 то мы получаем, что:
то мы получаем, что: 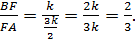
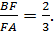
Ответ: 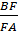
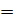
 .
.
II способ (с использованием теоремы Менелая)
Пусть 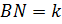 , тогда по условию (
, тогда по условию (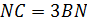 ):
): 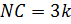 ; пусть
; пусть 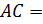
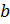 , тогда по условию МС=
, тогда по условию МС= 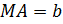 .
.
Прямая 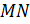 пересекает две стороны
пересекает две стороны 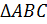 (
(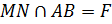 ,
, 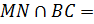
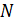 ) и продолжение третьей (
) и продолжение третьей (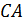 – луч,
– луч, 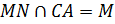 ), значит, по теореме Менелая:
), значит, по теореме Менелая: 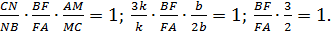 И, значит,
И, значит, 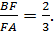
Ответ: 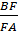
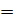
 .
.
Как видим, использование теоремы Менелая значительно упрощает решение этой задачи.
Приложение. Банк задач, для решения которых рекомендуется использовать теоремы Чевы, Менелая, Ван-Обеля и Симпсона
Катеты прямоугольного треугольника равны 9, 12 и гипотенуза равна 15. Найдите расстояние между точкой пересечения биссектрис и точкой пересечения медиан.
В треугольнике ABC медиана AK пересекает медиану BD в точке L. Найдите площадь треугольника ABC, если площадь четырехугольника KCDL равна 5.
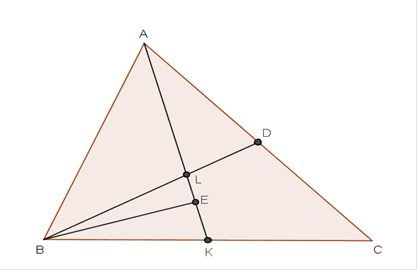
Через точку пересечения медиан треугольника ABC проходит прямая, пересекающая стороны AB и AC. Расстояния от вершин В и С до этой прямой равны b и с соответственно. Найдите расстояние от вершины А до этой прямой.
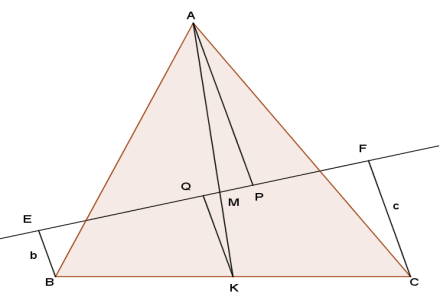
Через точку Р, лежащую на медиане СС1 треугольника АВС , проведены прямые АА1 и ВВ1 ( точки А1 и В1 лежат на сторонах ВС и СА соответственно). Докажите, что А1В1 ? АВ.
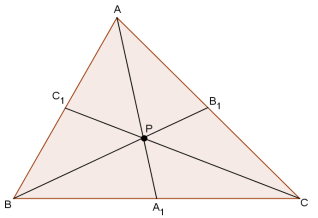
Прямая, соединяющая точку Р пересечения диагоналей четырехугольника ABCD с точкой Q пересечения прямых АВ и CD, делит сторону AD пополам. Докажите, что она делит пополам и сторону ВС.
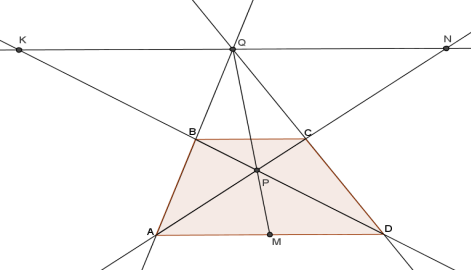
Из вершины С прямого угла треугольника АВС опущена высота СК, и в треугольнике АСК проведена биссектриса СЕ. Прямая, проходящая через точку В параллельно СЕ, пересекает СК в точке F. Докажите, что прямая EF делит отрезок АС пополам.
Библиографическая ссылка
Запольских М.В. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ТЕОРЕМ ЧЕВЫ И МЕНЕЛАЯ // Старт в науке. – 2020. – № 2.
;
URL: https://science-start.ru/ru/article/view?id=1854 (дата обращения: 04.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Чевы и Менелая
Работа учителя математики МБОУ СОШ № 29 г. Ставрополя
Емец Светланы Викторовны.

- Введение
- Краткая биография Чевы и Менелая
- Теоремы
- Решение задач
- Заключение
- Список литературы

- В курсе геометрии рассматриваются важные и интересные свойства геометрических фигур на плоскости, но многие удивительные соотношения и изящные геометрические факты не входят в основной курс.
- Работа посвящена теоремам Чевы и Менелая. Эти теоремы позволяют легко и изящно получить решение, в то время как традиционные подходы приводят к громоздким преобразованиям.
( Ceva Giovanni), родился 3.3.1648, Милан – умер 13.12.1734, Мантуя.
Итальянский математик. Главными предметами его занятий были геометрия и механика. Он написал сочинения: “De lineis rectis se invicem secantibus statica constructio” (Милан, 1678); “Opuscula mathematica de potentiis obliquis, de pendulis et vasis et de fluminibus” (там же, 1682); и несколько других. Самым замечательным из них было первое. В первой его части автор доказывает теорему Менелая и ряд сходных с нею теорем при помощи статического метода, основанного на свойствах центра тяжести системы точек. Прилагаемый к вопросам, в которых рассматриваются отношения между отрезками, образованными пересекающимися линиями друг на друге, он состоит в помещении в точках пересечения тяжестей, обратно пропорциональных соответствующим отрезкам, и в последующем за тем выводе отношения между тяжестями на основании принципа рычага в статике. Достаточно назвать известное в геометрии под именем теоремы Ц. предложение о произведениях отрезков, образованных на сторонах треугольника трансверсалями, проходящими через общую точку (произведение трех отрезков, не сходящихся попарно в одной общей точке, равно произведению трех других отрезков), и на подобное же предложение об отрезках, образованных на сторонах четырехугольника плоскостью, их пересекающею, если не все вершины четырехугольника лежат в одной плоскости. Во второй части идеи и теоремы, изложенные в 1-й, прилагаются к коническим сечениям. Наконец, прибавление занимается теоремами о площадях некоторых плоских фигур и об объемах и центрах тяжести тел вращения второго порядка. Его брат, Томмазо Ч., математик (1648 — 1737), иезуит. В 1695 г. изобрел инструмент для механического деления угла на три части. Написал: “De natura gravium” (1669); “De ratione aequilibri. De sectione geometrico-harmonica et arithmetica etc.” (1699); “Opuscula mathematica” (1699).

- Менела́й Александри́йский (Μενέλαος ὁ Αλεξανδρεύς, ок. 70 – от 140 н. э.) — древнегреческий математик и астроном. Время его жизни и деятельности определяется приведёнными в «Алмагесте» Птолемея двумя астрономическими наблюдениями, которые Менелай произвёл в Риме в первом году царствования Траяна , то есть в 98 г после Р. Х. .
- Главное сочинение Меналая — «Сферика» в трёх книгах. Его греческий оригинал утрачен, и содержание его известно по арабским, а также последующим вторичным латинским и еврейским переводам. В I книге дается определение сферического треугольника и связанных с ним понятий. В 39 предложениях этой книги речь идёт о свойствах сферических треугольников. В 21 предложении II книги рассматриваются свойства системы параллельных кругов на поверхности сферы при пересечении их разными большими кругами. Эта книга опирается на «Сферику» Феодосия . Книге III предшествуют леммы о составных отношениях, на которых строятся дальнейшие доказательства. Эта книга открывается теоремой о полном четырёхстороннике (известной также как «теорема шести величин» или «теорема о трансверсалях»). Она доказывается сначала для плоского случая, а затем переносится центральным проектированием на сферу. При этом Менелай формулирует её сферический вариант не на языке отношений синусов, как это стали делать впоследствии Ибн Ирак и другие математики стран ислама, но на языке отношений хорд.

- Менелаем были написаны не дошедшие до нас сочинения «О вычислении хорд» в 6 книгах, «Начала геометрии» в 3 книгах, «Книга о треугольнике», «Книга о заходах знаков зодиака».
- Менелай изучал кривые высших порядков. Особенным его вниманием, по словам Паппа , пользовалась одна кривая, которая была названа им «необыкновенной линией» (παραδοξος γραμμή). Какая это была кривая, из слов Паппа, однако же, определить нельзя. По мнению П. Таннери, она представляла собой кривую, образующуюся при пересечении сферы и кругового цилиндра, радиус которого вдвое меньше радиуса сферы, а образующая проходит через центр. Эта кривая возникает в решении задачи об удвоении куба, принадлежащем Архиту Тарентскому , а из трактата братьев Бану Муса известно, что Менелай занимался этим решением.
- Менелаю принадлежала «Книга о подразделении составных тел», посвящённая определению удельных весов тел. Эту книгу цитирует ал-Хазини в своей «Книге весов мудрости».
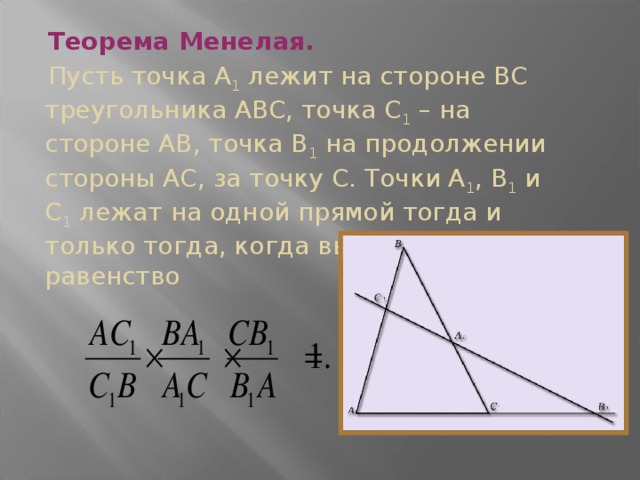
Пусть точка А 1 лежит на стороне ВС треугольника АВС, точка С 1 – на стороне АВ, точка В 1 на продолжении стороны АС, за точку С. Точки А 1 , В 1 и С 1 лежат на одной прямой тогда и только тогда, когда выполняется равенство

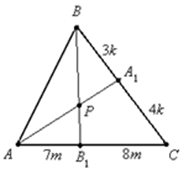
Пусть в треугольнике АВС точка А 1 лежит на стороне ВС, точка В 1 на стороне АС, точка С 1 – на стороне АВ. Отрезки АА 1 , ВВ 1 , СС 1 пересекаются в одной точке тогда и только тогда, когда выполняется равенство
Отрезки прямых АА 1 , ВВ 1 , СС 1 – «чевианы» названы по имени автора теоремы. Медианы, биссектрисы, высоты – примеры чевиан.

Решение Задач по теореме Менелая
1. Пусть AD — медиана треугольника ABC. На стороне AD взята точка К так, что АК : KD = = 3:1. Прямая ВК разбивает треугольник ABC на два. Найдите отношение площадей этих треугольников.
Решение. Пусть AD = DC = a, KD = т; тогда АК = Зт. Пусть Р — точка пересечения прямой ВК со стороной АС. Необходимо
найти отношение . Так как треугольники АВР
и РВС имеют равные высоты, проведенные из вершины В, то =
По теореме Менелая для треугольника ADC и секущей РВ имеем:
Итак, S ABP : S BPC = 3 : 2.
Ответ: 3 : 2
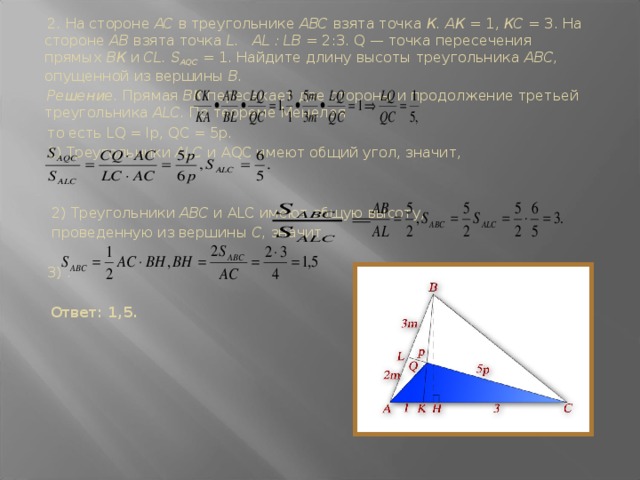
2. На стороне АС в треугольнике ABC взята точка К. АК = 1, КС = 3. На стороне АВ взята точка L. AL : LB = 2:3. Q — точка пересечения прямых ВК и CL. S AQC = 1. Найдите длину высоты треугольника ABC, опущенной из вершины В.
Решение. Прямая ВК пересекает две стороны и продолжение третьей треугольника ALC. По теореме Менелая
то есть LQ = lp, QC = 5р.
1) Треугольники ALC и AQC имеют общий угол, значит,
2) Треугольники ABC и ALC имеют общую высоту,
проведенную из вершины С, значит,

3. Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделана центром окружности, вписанной в треугольник.
Решение. Пусть в треугольнике ABC АВ = 5, ВС = 7, АС = 6. Угол ВАС
лежит против большей стороны в треугольнике ABC, значит, угол ВАС — больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Пусть О — точка пересечения биссектрис. Необходимо найти АО: OD. Так как AD —биссектриса треугольника ABC, то , то есть
BD = 5k, DC = 6k. Так как BF — биссектриса треугольника ABC, то
, то есть AF = 5т, FC = 7т.
Прямая BF пересекает две стороны и продолжение третьей треугольника ADC. По теореме Менелая
Ответ: 11 : 7.

4. Биссектрисы BE и AD треугольника ABC пересекаются в точке Q. Найдите площадь треугольника ABC, если , 2АС = ЗАВ, 3BC = 4AB.
Решение. Пусть АВ = а,
тогда АС = а, ВС = а.
AD — биссектриса треугольника ABC, тогда
то есть BD = 2р, DC = Зр.
BE — биссектриса треугольника ABC, тогда
AE=3k, ЕС = 4к.
В треугольнике ВEС прямая AD пересекает 2 стороны и продолжение третьей стороны. По теореме Менелая
то есть EQ = 9m, QB = 14m.
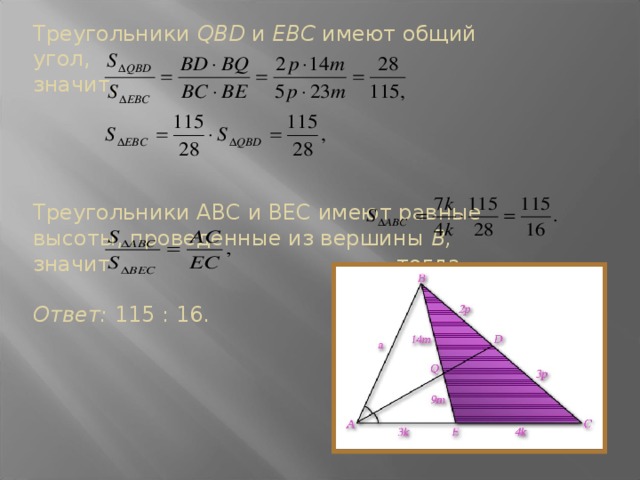
Треугольники QBD и ЕВС имеют общий угол,
Треугольники ABC и ВЕС имеют равные высоты, проведенные из вершины В, значит , тогда
Ответ: 115 : 16.
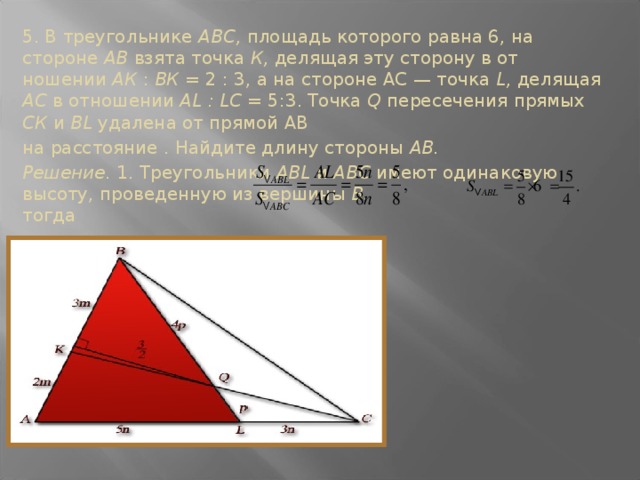
5. В треугольнике ABC, площадь которого равна 6, на стороне АВ взята точка К, делящая эту сторону в отношении АК : ВК = 2 : 3, а на стороне АС — точка L, делящая АС в отношении AL : LC = 5:3. Точка Q пересечения прямых СК и BL удалена от прямой АВ
на расстояние . Найдите длину стороны АВ.
Решение. 1. Треугольники ABL и ABC имеют одинаковую высоту, проведенную из вершины В. тогда
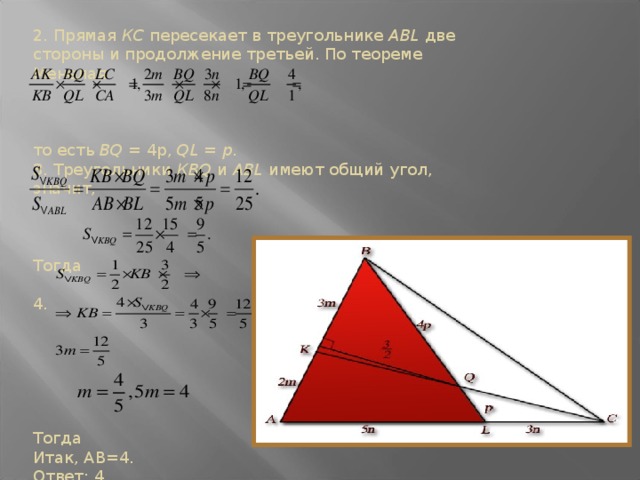
2. Прямая КС пересекает в треугольнике ABL две стороны и продолжение третьей. По теореме Менелая
то есть BQ = 4p, QL = p.
3. Треугольники КВQ и ABL имеют общий угол, значит,

Решение задач по теореме Чевы Джованни
Используя теорему Чевы доказываются следующие утверждения:
1.Медианы треугольника пересекаются в одной точке.
2.Биссектрисы треугольника пересекаются в одной точке.
3.Высоты треугольника (или их продолжения) пересекаются в одной точке.
1. Докажите теорему: если в треугольник вписана окружность, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке.
Пусть А 1 , В 1 и С 1 – точки касания вписанной окружности треугольника АВС. Для того, чтобы доказать, что отрезки АА 1 , ВВ 1 и СС 1 пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:
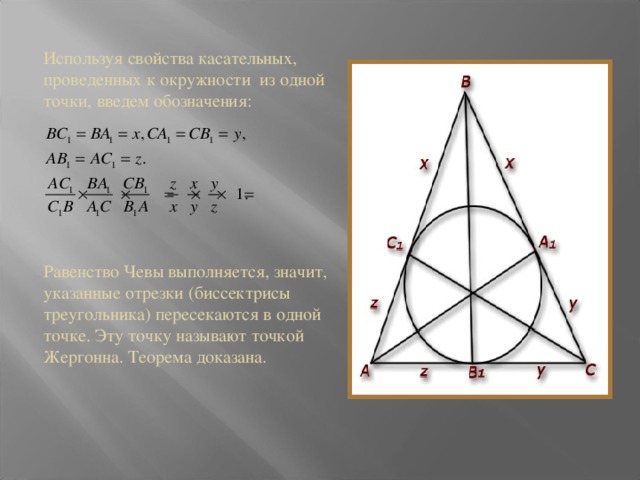
Используя свойства касательных, проведенных к окружности из одной точки, введем обозначения:
Равенство Чевы выполняется, значит, указанные отрезки (биссектрисы треугольника) пересекаются в одной точке. Эту точку называют точкой Жергонна. Теорема доказана.

2.Докажите теорему: медианы треугольника пересекаются в одной точке; точка пересечения делит каждую из них в отношении 2:1, считая от вершины.
Доказательство. Пусть AL 1 ВL 2 , CL 3 — медианы треугольника ABC. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что
Тогда по теореме Чевы (обратной) отрезки AL 1, ВL 2 и СL 3 пересекаются в одной точке. Имеем:
Итак, доказано, что медианы треугольника пересекаются в одной точке.

2. Пусть О — точка пересечения медиан. Прямая L 3 С пересекает две стороны треугольника АВL 2 и продолжение третьей стороны этого треугольника. По теореме Менелая
Рассматривая теорему Менелая для треугольников AL C и АL 3 С, мы получаем, что ,
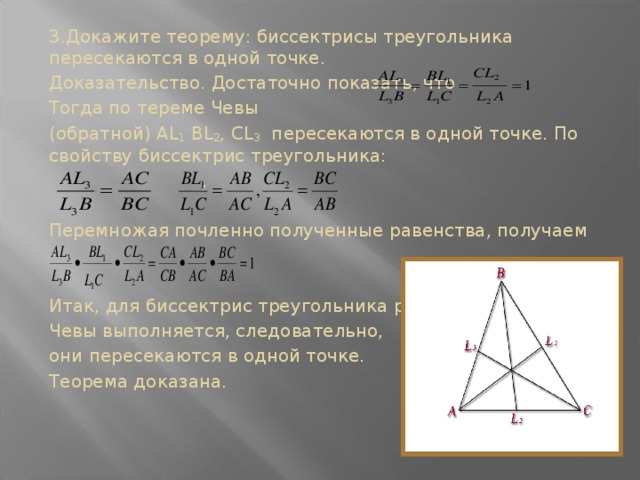
3.Докажите теорему: биссектрисы треугольника пересекаются в одной точке.
Доказательство. Достаточно показать, что
Тогда по тереме Чевы
(обратной) AL 1 BL 2 , CL 3 пересекаются в одной точке. По свойству биссектрис треугольника:
Перемножая почленно полученные равенства, получаем
Итак, для биссектрис треугольника равенство
Чевы выполняется, следовательно,
они пересекаются в одной точке.

1.Для решения задач необходимо находить треугольник, удовлетворяющий этим теоремам.
2.При составлении равенства Менелая можно записывать, начиная с любой вершины треугольника, в любом направлении, а также надо переходить от вершины к вершине через точку пересечения секущей линии с этой стороной или ее продолжением. Заканчивать необходимо в той же вершине с которой начали.
3.Утверждения и теоремы, доказанные в курсе планиметрии, можно доказать используя теорему Чевы.
4.В работе размещены задачи, которые были предложены при поступлении в ВУЗы и при проведении олимпиад. Этот материал был изложен на спецкурсе по математике, и может быть использован при подготовке к экзаменам.

1.Геометрия 7-9 Л.С. Атанасян, В.Ф. Бутузов, Москва, «Просвещение» 1994 г.
2.Математика. Подготовка к тестированию. Г.Г. Мамонтова, Минск ООО «Новое знание» 2005 г.
3. Атанасян Л.С. Бутузов В.Ф.и др.Геометрия: Учеб. пособие для7-9 кл.общеобразоват. учреждений- М.: Просвещение ,1999
4. Балк М. Б. Болтянский В. Г. Геометрия масс -М.: Наука, 1987
5. Балк М. Б. Болтянский В. Г Центр тяжести облегчает решение .стр.32-41 Проложение к журналу КВАНТ №1\95
6. Всероссийские математические олимпиады школьников. -М., Просвещение ,1992
7. Глайзер Г.И. История математики в средней школе .Пособие для учителей .-М.,Просвещение,1970
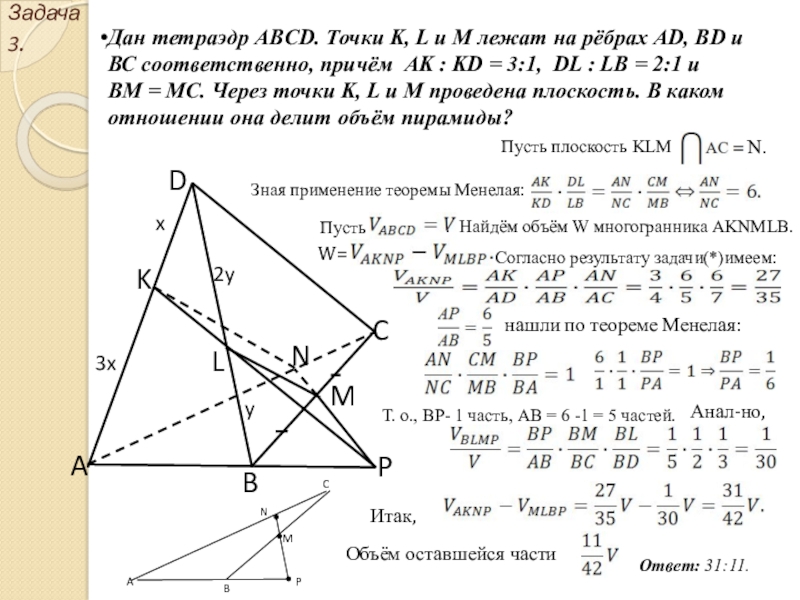
Слайд 10Дан тетраэдр ABCD. Точки K, L и M лежат на рёбрах
AD, BD и ВС соответственно, причём AK : KD = 3:1, DL : LB = 2:1 и
ВМ = МС. Через точки K, L и M проведена плоскость. В каком отношении она делит объём пирамиды?
Пусть плоскость KLM
Зная применение теоремы Менелая:
. Найдём объём W многогранника AKNMLB.
Согласно результату задачи(*)имеем:
нашли по теореме Менелая:
Т. о., ВР- 1 часть, АВ = 6 -1 = 5 частей.
Объём оставшейся части
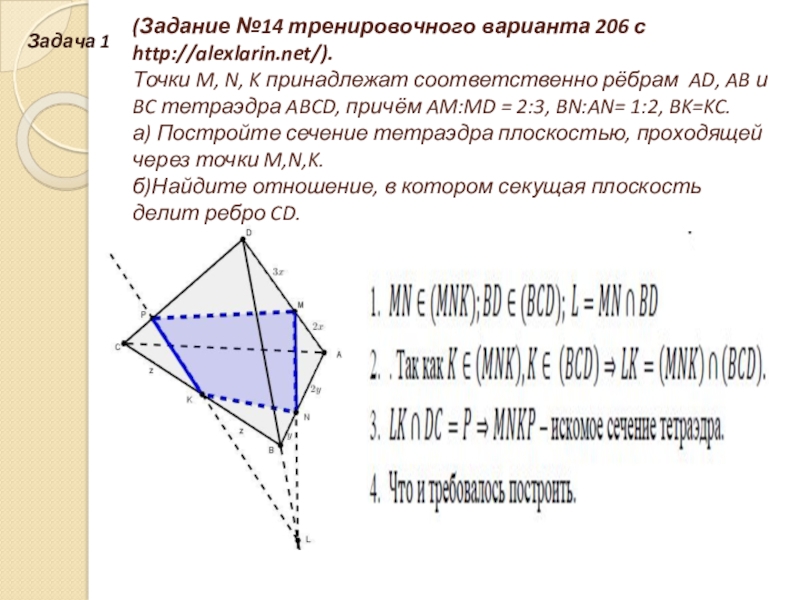
Слайд 4(Задание №14 тренировочного варианта 206 с http
соответственно рёбрам AD, AB и BC тетраэдра ABCD, причём AM:MD = 2:3, BN:AN= 1:2, BK=KC.
а) Постройте сечение тетраэдра плоскостью, проходящей через точки M,N,K.
б)Найдите отношение, в котором секущая плоскость делит ребро CD.
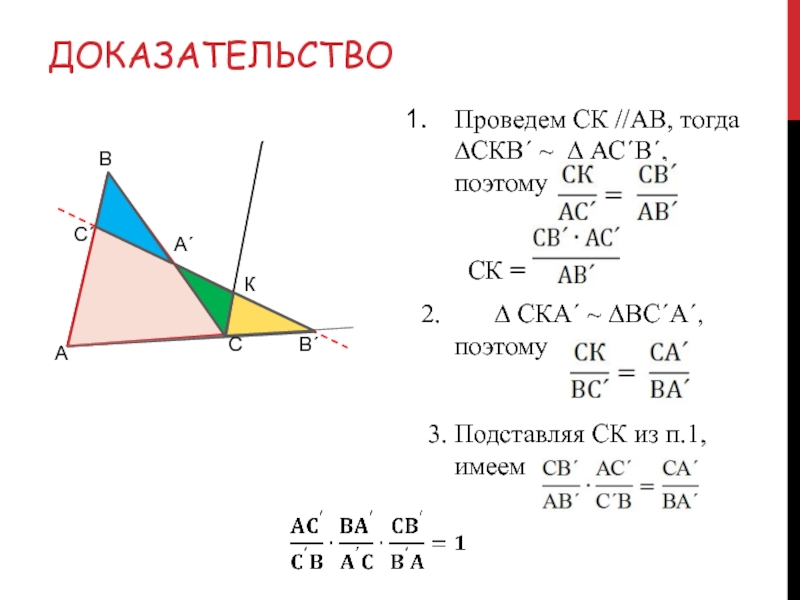
Слайд 4Доказательство Проведем СК //АВ, тогда ∆СКВ´ ~ ∆ АС´В´, поэтому
СК =
2. ∆ СКА´ ~ ∆ВС´А´, поэтому
3. Подставляя СК из п.1, имеем
Слайд 1Теорема Менелая в тетраэдрахУчитель математики высшей квалификационной категории
МБОУ «Гимназия №4 им. А.С. Пушкина»

Показать применение теоремы Менелая к тетраэдрам;
2. развить стереометрическое мышление
на более высоком уровне;
3. помочь учителю оценить свой потенциал с точки зрения образовательной перспективы;
4. способствовать интеллектуальному развитию учителя, формированию качеств мышления, характерных для математической деятельности.
ЦЕЛЬ: помочь учителю-предметнику в организации подготовки старшеклассников к успешному решению экзаменационных стереометрических задач

Слайд 6ЗамечаниеПри решении задач , применяя теорему Менелая, следует обратить внимание на

Слайд 6
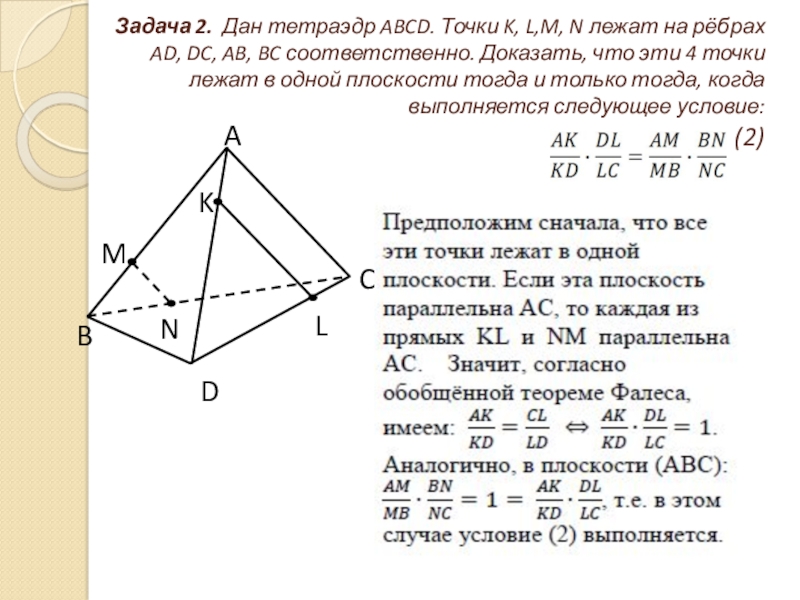
Задача 2. Дан тетраэдр ABCD. Точки K, L,M, N лежат
на рёбрах AD, DC, AB, BC соответственно. Доказать, что эти 4 точки лежат в одной плоскости тогда и только тогда, когда выполняется следующее условие:
(2)
” m n ТЕОРЕМА МЕНЕЛАЯ названа по имени древнегреческого учёного Менелая (I в. ), доказавшего её для сферического треугольника Пусть М; Р; К – три точки,” — Транскрипт
m n
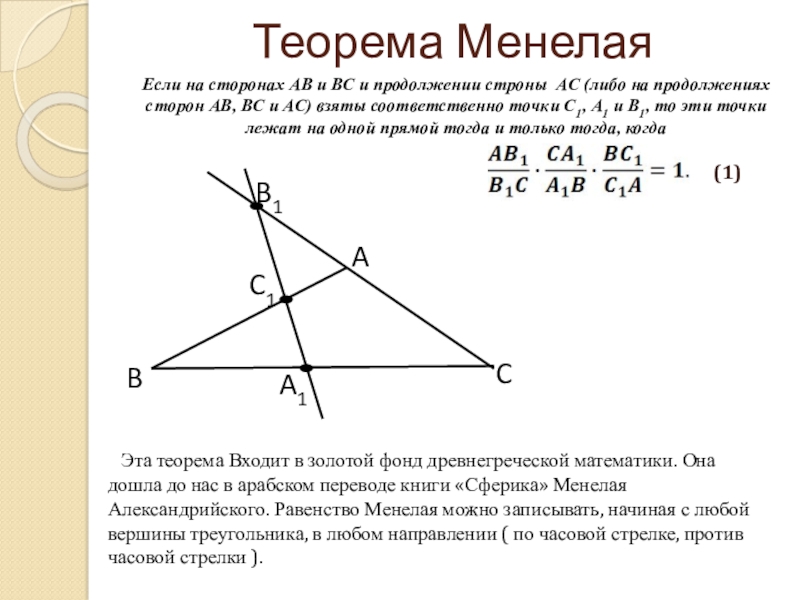
ТЕОРЕМА МЕНЕЛАЯ названа по имени древнегреческого учёного Менелая (I в.), доказавшего её для сферического треугольника Пусть М; Р; К – три точки, лежащие соответственно на сторонах СА; АВ и ВС треугольника АВС или на их продолжениях. Точки М; Р; К тогда и только тогда лежат на одной прямой, если
А В С М Р К
А В С М Р К О Е Д Доказательство необходимого условия
РЕШАЕМ ЗАДАЧУ ПО ГОТОВОМУ ЧЕРТЕЖУ 2 А В С М а а К в в N В каком отношении точка К делит основание треугольника?
Самостоятельная работа 1 вариант 2 вариант На сторонах АВ и АС В треугольнике АВС треугольника АВС даны биссектриса АД делит соответственно точки ВС в отношении 2:1. М и N так, что В каком отношении В каком отношении точка медиана СЕ делит эту S – пересечения отрезков биссектрису? ВN и СМ делит каждый из этих отрезков?
РЕШЕНИЕ ЗАДАЧИ 1-го ВАРИАНТА А В С М N S а 2 а в 2 в К треугольнику АВN применим теорему Менелая. Получим: К треугольнику АМС применим теорему Менелая. Получим:
РЕШЕНИЕ ЗАДАЧИ 2-го ВАРИАНТА В К треугольнику АВД применим теорему Менелая. Получим: А С Д 2 а а Е ДО : ОА =1 :3
ЗАДАЧА 3 В а а С К А Д К М Р
ЗАДАЧА: В треугольнике АВС отрезки АД и ВМ, проведённые из вершин А и В соответственно к сторонам ВС и АС, пересекаясь в точке Р, делятся в отношении АР:РД=3:2 и ВР:РМ=4:5. В каком отношении точки Д и М делят стороны треугольника, считая от С?
А В С Д М 3 к 2 к 4 р 5 р Р
Слайд 3Теорема МенелаяЕсли на сторонах АВ и ВС и продолжении строны АС
(либо на продолжениях сторон АВ, ВС и АС) взяты соответственно точки С1, А1 и В1, то эти точки лежат на одной прямой тогда и только тогда, когда
Эта теорема Входит в золотой фонд древнегреческой математики. Она дошла до нас в арабском переводе книги «Сферика» Менелая Александрийского. Равенство Менелая можно записывать, начиная с любой вершины треугольника, в любом направлении ( по часовой стрелке, против часовой стрелки ).
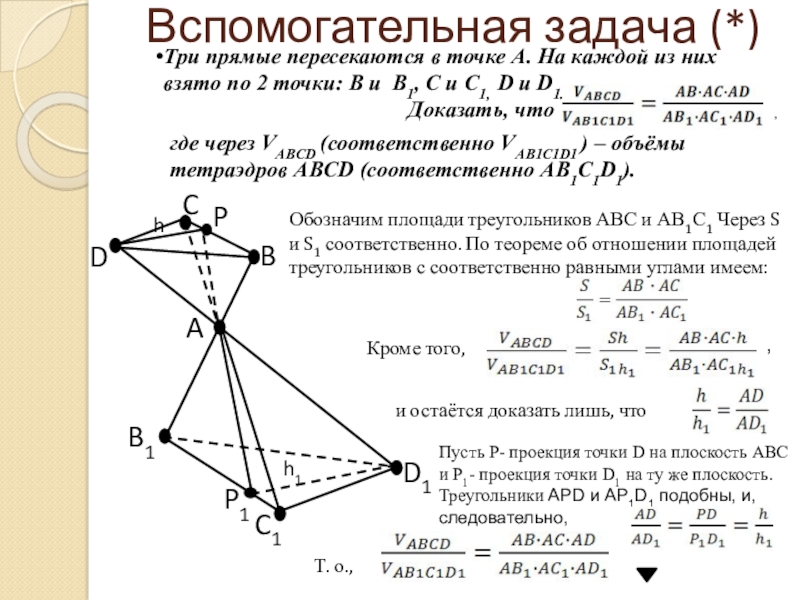
Слайд 9Вспомогательная задача (*)Три прямые пересекаются в точке А. На каждой из
них взято по 2 точки: В и В1, С и С1, D и D1.
Доказать, что
где через VABCD (соответственно VAB1C1D1 ) – объёмы тетраэдров ABCD (соответственно AB1C1D1).
Обозначим площади треугольников АВС и АВ1С1 Через S и S1 соответственно. По теореме об отношении площадей треугольников с соответственно равными углами имеем:
и остаётся доказать лишь, что
Пусть Р- проекция точки D на плоскость АВС и Р1- проекция точки D1 на ту же плоскость. Треугольники АPD и АP1D1 подобны, и, следовательно,
Теорема Менелая Теория Тренажеры Задачи

Теорема Менелая. • Теория. • Тренажеры. • Задачи.
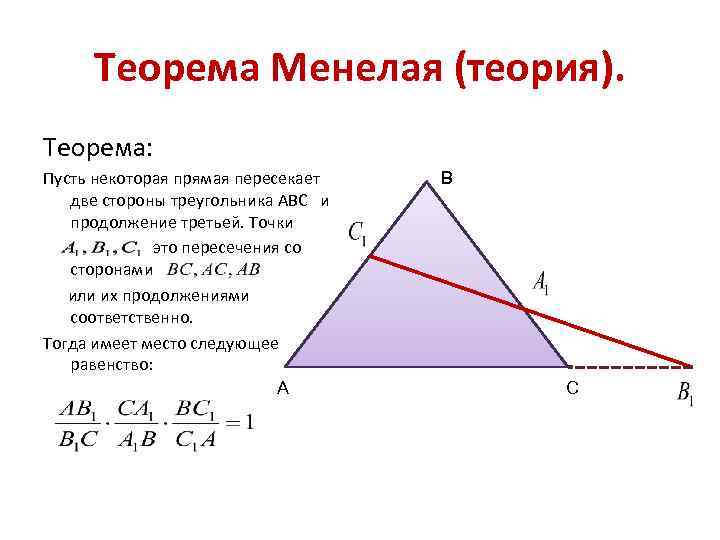
Теорема Менелая (теория). Теорема: Пусть некоторая прямая пересекает две стороны треугольника АВС и продолжение третьей. Точки это пересечения со сторонами или их продолжениями соответственно. Тогда имеет место следующее равенство: А В С
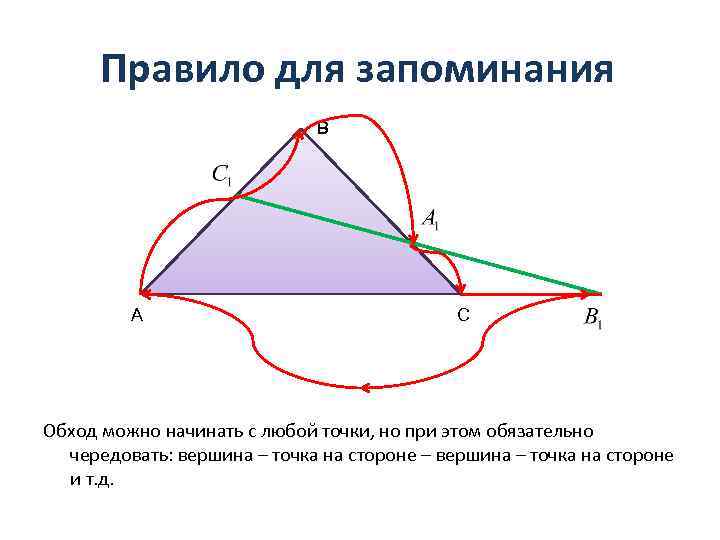
Правило для запоминания В А С Обход можно начинать с любой точки, но при этом обязательно чередовать: вершина – точка на стороне – вершина – точка на стороне и т. д.
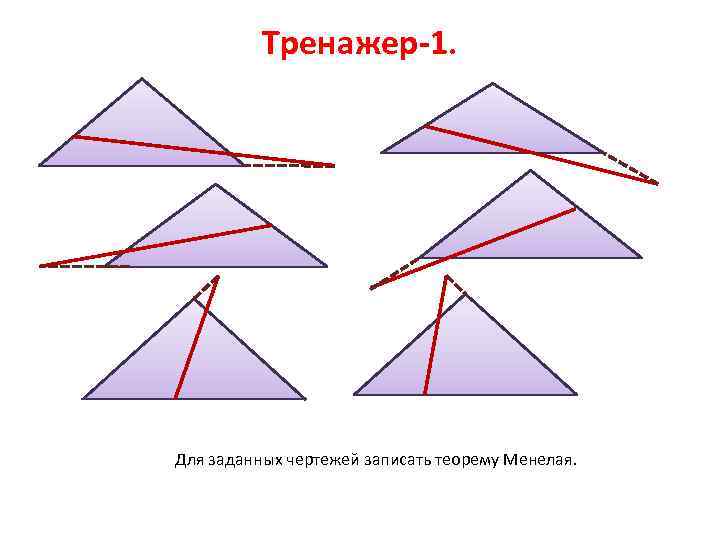
Тренажер-1. Для заданных чертежей записать теорему Менелая.
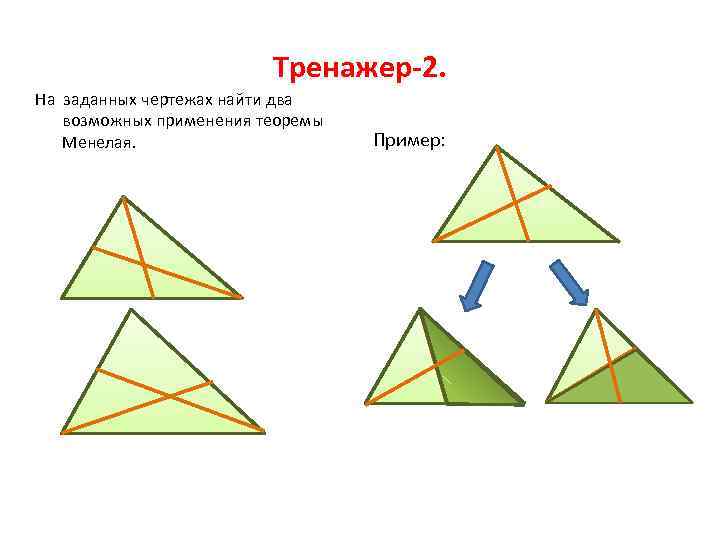
Тренажер-2. На заданных чертежах найти два возможных применения теоремы Менелая. Пример:
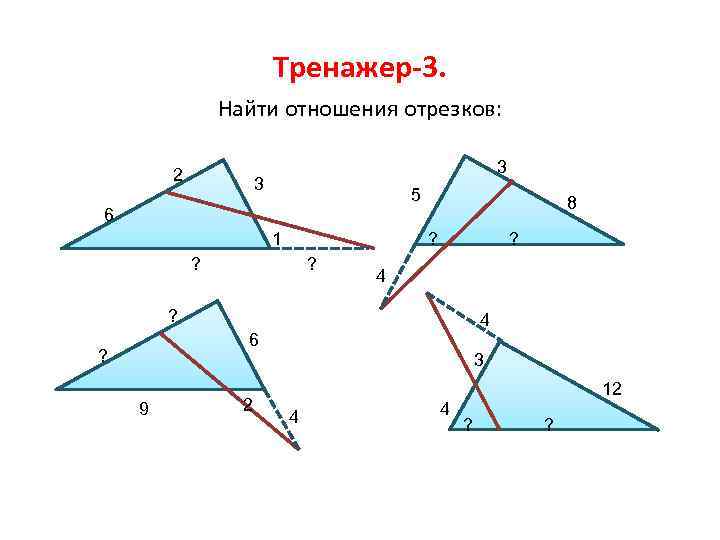
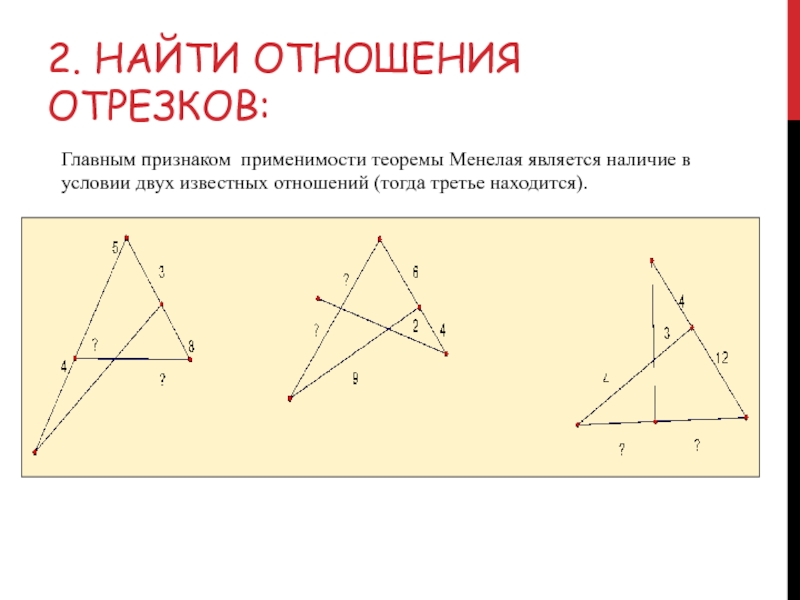
Тренажер-3. Найти отношения отрезков: 2 3 3 5 8 6 1 ? ? 4 6 ? 3 9 2 12 4 4 ? ?
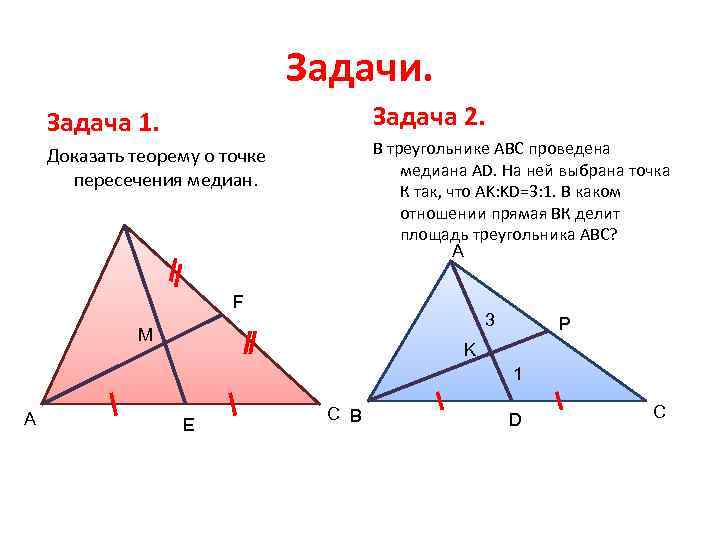
Задачи. Задача 2. Задача 1. В треугольнике АВС проведена медиана AD. На ней выбрана точка К так, что AK: KD=3: 1. В каком отношении прямая ВК делит площадь треугольника АВС? A Доказать теорему о точке пересечения медиан. F 3 M Р K 1 А Е С B D С
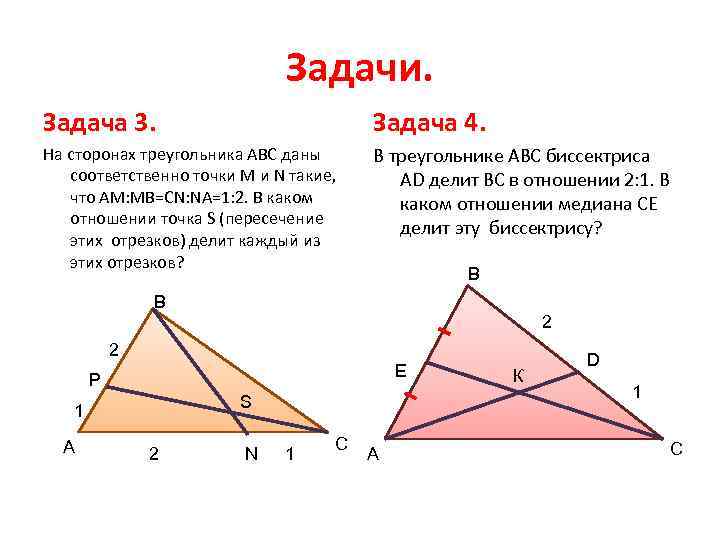
Задачи. Задача 3. Задача 4. На сторонах треугольника АВС даны соответственно точки М и N такие, что АМ: МВ=СN: NA=1: 2. В каком отношении точка S (пересечение этих отрезков) делит каждый из этих отрезков? В треугольнике АВС биссектриса AD делит ВС в отношении 2: 1. В каком отношении медиана СЕ делит эту биссектрису? B B 2 2 Е Р S 1 A 2 N 1 С A К D 1 С

Задачи. В y 3 x S=3 К x 2 z S=1 z А S=2 Q L 2 y S=6 С Задача 5. Решение: В треугольнике АВС на стороне 1) Применим теорему Менелая АВк взята точка ABL: что К так, треугольнику АК: ВК=1: 3, а на стороне ВС взята точка L так, что CL: BL=2: 1. Пусть Q – точка 2) Найдем пересеченияплощадь AL и CК. прямых треугольника ABQ: Найти площадь треугольника АВС, если площадь треугольника BQL равна 2. 3) Используем отношение площадей треугольников ABL и ALC: Ответ: площадь треугольника равна 9.
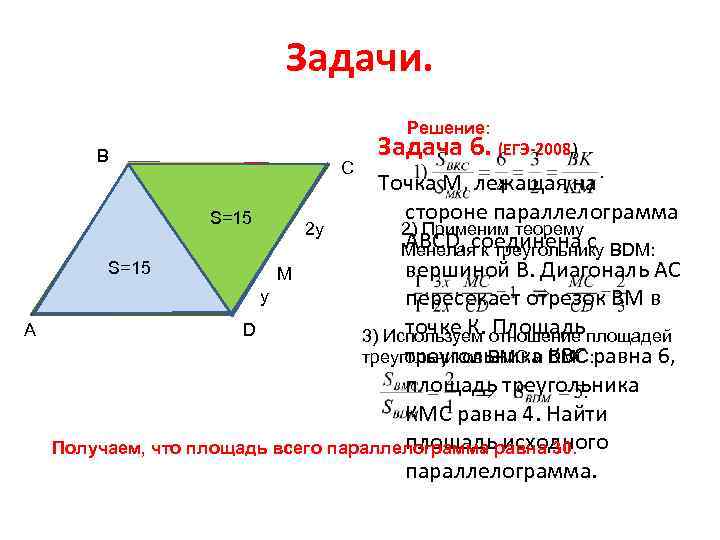
Задачи. Решение: B Точка М, лежащая на 3 x стороне параллелограмма 2 y 2) Применим теорему ABCD, соединена с S=5 K 2 x Менелая к треугольнику BDM: O S=15 вершиной В. Диагональ АС M y пересекает отрезок ВМ в точке К. Площадь D 3) Используем отношение площадей треугольника КВС треугольников BMС и DMC: равна 6, площадь треугольника КМС равна 4. Найти площадь исходного Получаем, что площадь всего параллелограмма равна 30. параллелограмма. S=6 S=10 S=15 S=4 А C Задача 6. (ЕГЭ-2008)
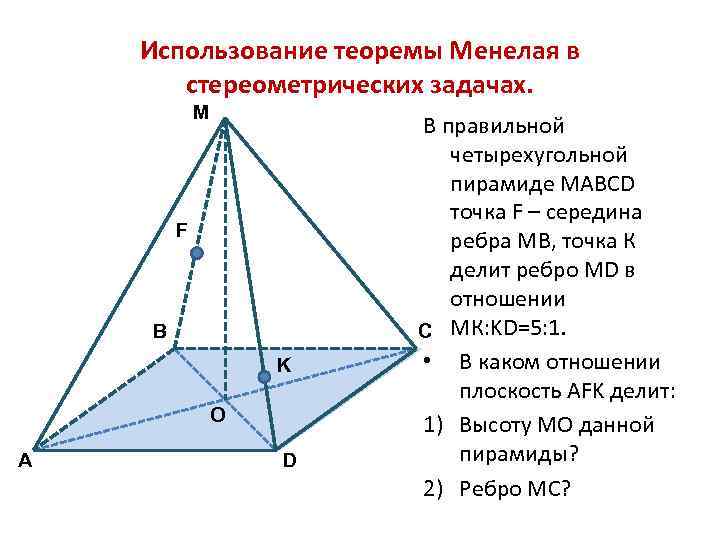
Использование теоремы Менелая в стереометрических задачах. M F B K O A D В правильной четырехугольной пирамиде MABCD точка F – середина ребра МВ, точка К делит ребро МD в отношении C МК: KD=5: 1. • В каком отношении плоскость АFK делит: 1) Высоту МО данной пирамиды? 2) Ребро МС?
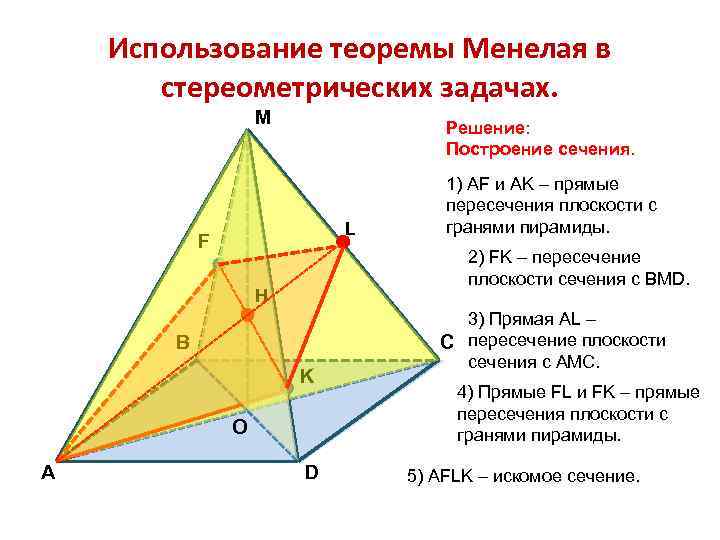
Использование теоремы Менелая в стереометрических задачах. M Решение: Построение сечения. L F 2) FK – пересечение плоскости сечения с BMD. Н B K O A 1) AF и AK – прямые пересечения плоскости с гранями пирамиды. D 3) Прямая AL – C пересечение плоскости сечения с АМС. 4) Прямые FL и FK – прямые пересечения плоскости с гранями пирамиды. 5) AFLK – искомое сечение.
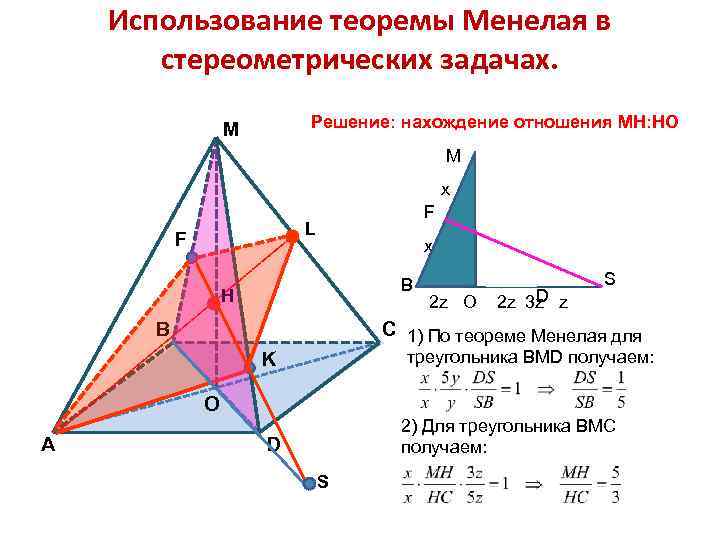
Использование теоремы Менелая в стереометрических задачах. Решение: нахождение отношения МН: НО M M x F L F x B Н B 5 y Н K y 2 z О D 2 z 3 z z S C 1) По теореме Менелая для треугольника ВMD получаем: K O A 2) Для треугольника ВМС получаем: D S
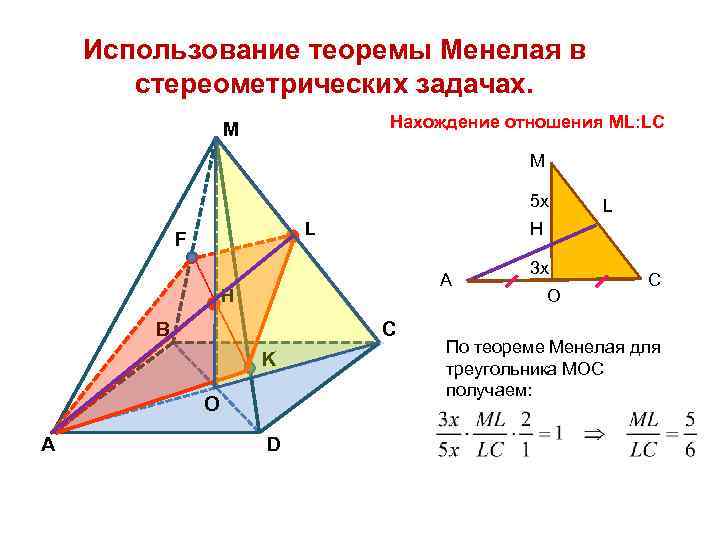
Использование теоремы Менелая в стереометрических задачах. Нахождение отношения ML: LC M М 5 x L F Н А Н B C K O A D L 3 x О C По теореме Менелая для треугольника МОС получаем:
Слайд 13План обнаружения теоремы Менелая На сложном рисунке необходимо по двум имеющимся отношениям
отрезков выделить (желательно цветом) прямые на которых эти отрезки лежат (линии сторон будущего треугольника), а после заниматься подбором секущей.

Слайд 14Решить задачу с помощью теоремы Менелая
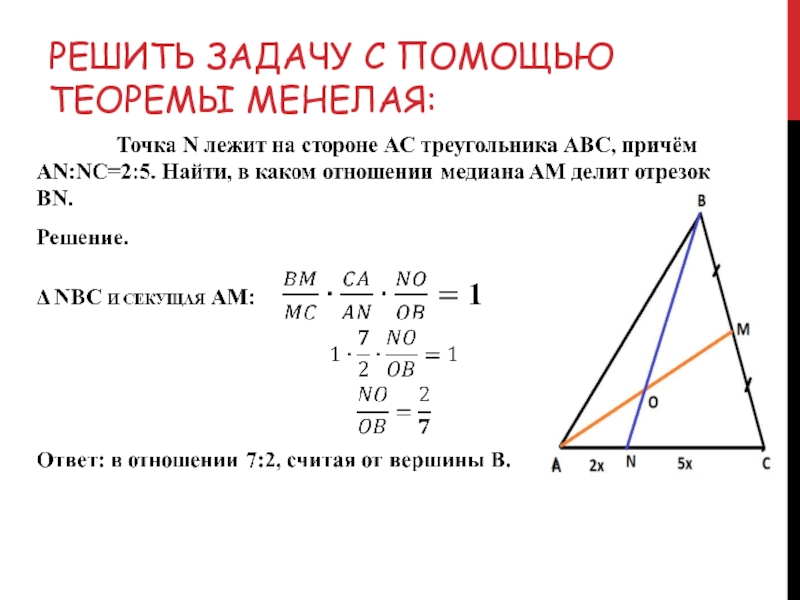
Слайд 5Теорема (обратная теореме Менелая)

Главным признаком применимости теоремы Менелая является наличие
в условии двух известных отношений (тогда третье находится).
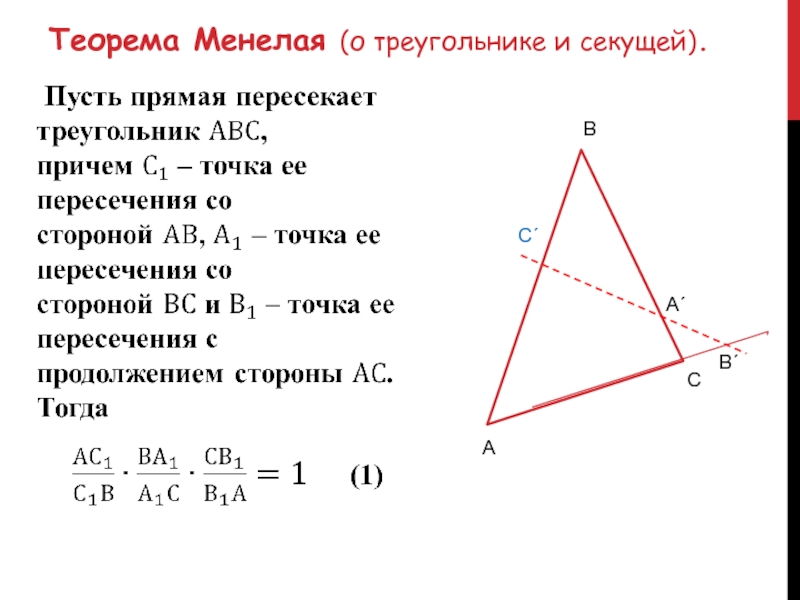
Слайд 3Теорема Менелая (о треугольнике и секущей). АС´ВА´СВ´
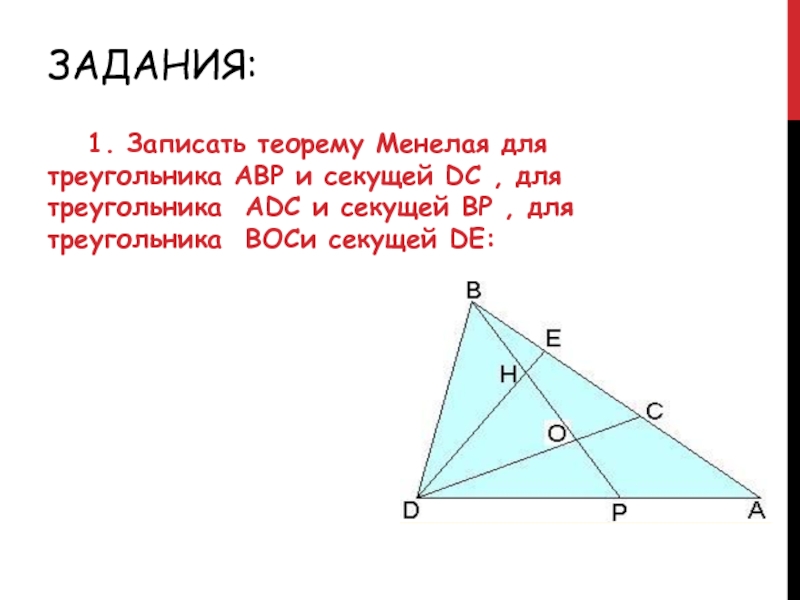
Записать теорему Менелая для треугольника АВР и секущей DC ,
для треугольника ADC и секущей BP , для треугольника BOCи секущей DE:
Слайд 2 Менелай Александрийский ( , I в. ) – древнегреческий математик и астроном. Автор работ
по сферической тригонометрии: написал 6 книг о вычислении хорд и 3 книги “Сферики’’, сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема Менелая.
